
分析 (Ⅰ)根据平面向量的坐标运算与共线定理,列出方程求出λ的值;
(Ⅱ)根据平面向量的坐标运算与互相垂直的数量积为0,列出方程求出k的值.
解答 解:(Ⅰ)∵向量$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(-1,3),
∴3$\overrightarrow{a}$+2$\overrightarrow{b}$=(4,9),
-$\overrightarrow{a}$+λ$\overrightarrow{b}$=(-2-λ,3λ-1),
又(3$\overrightarrow{a}$+2$\overrightarrow{b}$)∥(-$\overrightarrow{a}$+λ$\overrightarrow{b}$),
∴4(3λ-1)-9(-2-λ)=0,
解得λ=-$\frac{2}{3}$;
(Ⅱ)∵2$\overrightarrow{a}$-$\overrightarrow{b}$=(5,-1),
k$\overrightarrow{a}$+$\overrightarrow{b}$=(2k-1,k+3),
且(2$\overrightarrow{a}$-$\overrightarrow{b}$)⊥(k$\overrightarrow{a}$+$\overrightarrow{b}$),
∴5(2k-1)-(k+3)=0,
解得k=$\frac{8}{9}$.
点评 本题考查了平面向量的坐标运算与向量的共线和垂直的应用问题,是基础题目.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 | 5 |
| y | 2.9 | 3.3 | 3.6 | 4.4 | 5.1 |
| u | 1 | 2 | 3 | 4 | 5 |
| v | 25 | 20 | 21 | 15 | 13 |
| A. | 变量x与y正相关,u与v正相关 | B. | 变量x与y负相关,u与v正相关 | ||
| C. | 变量x与y负相关,u与v负相关 | D. | 变量x与y正相关,u与v负相关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{2π}{3}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
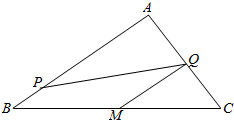 如图,在Rt△ABC中,AB=4,AC=3,∠A=90°,$\overrightarrow{AP}$=m$\overrightarrow{PB}$,$\overrightarrow{AQ}$=n$\overrightarrow{QC}$,m,n>0,且满足$\frac{1}{m}$+$\frac{1}{n}$=$\frac{1}{2}$,M是BC的中点,对任意的λ∈R,|λ•$\overrightarrow{QP}$+$\overrightarrow{QM}$|的最小值记为f(m),则对任意m>0,f(m)的最大值为$\frac{1}{2}$.
如图,在Rt△ABC中,AB=4,AC=3,∠A=90°,$\overrightarrow{AP}$=m$\overrightarrow{PB}$,$\overrightarrow{AQ}$=n$\overrightarrow{QC}$,m,n>0,且满足$\frac{1}{m}$+$\frac{1}{n}$=$\frac{1}{2}$,M是BC的中点,对任意的λ∈R,|λ•$\overrightarrow{QP}$+$\overrightarrow{QM}$|的最小值记为f(m),则对任意m>0,f(m)的最大值为$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日需求量n(瓶) | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 频数 | 5 | 5 | 8 | 12 | 10 | 6 | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com