
| A. | sina=acosb | B. | sinb=-bsina | C. | cosa=bsinb | D. | sina=-acosb |
分析 化简f(x),得方程$\frac{|sinx|}{x}=k$有两个根,即函数y=|sinx|和函数y=kx在(0,+∞)上有两个交点,画出函数图象,利用导数求切线即可.
解答 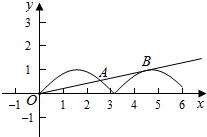 解:f(x)=$\frac{|cos(x-\frac{π}{2})|}{x}$-k=$\frac{|sinx|}{x}$,
解:f(x)=$\frac{|cos(x-\frac{π}{2})|}{x}$-k=$\frac{|sinx|}{x}$,
∵f(x)=$\frac{|cos(x-\frac{π}{2})|}{x}$-k在(0,+∞)上有两个不同的零点a,b(a<b),
∴f(x)=$\frac{|sinx|}{x}$-k=0在(0,+∞)上有两个不同的根a,b(a<b),
即|sinx|=kx有两个根,
∴函数y=|sinx|和函数y=kx在(0,+∞)上有两个交点,x>0且k>0,画出两个函数的图象,
则函数y=|sinx|和函数y=kx在(0,π)上有一个交点A(a,sina),在(π,2π)上有一个切点B(b,-sinb)时满足题意,
a,b是方程的根.
当x∈(π,2π)时,f(x)=|sinx|=-sinx,f′(x)=-cosx,
∴在B处的切线为y+sinb=f′(b)(x-b),将x=0,y=0代入方程,得sinb=-b×(-cosb),
∴$\frac{sinb}{b}$=cosb,
∵O,A B三点共线,
∴$\frac{sina}{a}$=$\frac{-sinb}{b}$,
∴$\frac{sina}{a}$=-cosb,
∴sina=-acosb.
故选:D.
点评 本题借助图象考查了方程的根,函数的零点,以及导数的知识.把方程转化为函数的交点,利用数形结合是解题关键.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 000名学生是总体 | B. | 每个学生是个体 | ||
| C. | 1 000名学生的成绩是一个个体 | D. | 样本的容量是100 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
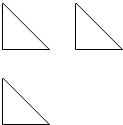 某几何体的三视图如图所示(均为直角边长为2的等腰直角三角形),则该几何体的表面积为( )
某几何体的三视图如图所示(均为直角边长为2的等腰直角三角形),则该几何体的表面积为( )| A. | 4+4$\sqrt{2}$ | B. | 4+4$\sqrt{3}$ | C. | 6+2$\sqrt{3}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x轴对称 | B. | y轴对称 | C. | 原点对称 | D. | 直线y=x对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 12π | B. | 8π | C. | $\frac{8π}{3}$ | D. | $\frac{20π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=\sqrt{x^2},y={(\sqrt{x})^2}$ | B. | $y=\sqrt{x-1}×\sqrt{x+1},y=\sqrt{{x^2}-1}$ | ||
| C. | $y=1,y=\frac{x}{x}$ | D. | $y=\left\{\begin{array}{l}x,x≥0\\-x,x<0\end{array}\right.$y=|x| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com