
(本小题满分l2分) 已知函数f(x)=ax3+bx2-3x在x=±1处取得极值.
(1)求函数f(x)的解析式;
(2)求证:对于区间[-1,1]上任意两个自变量的值x1,x2,都有|f(x1)-f(x2)|≤4;
(3)若过点A(1,m)(m≠-2)可作曲线y=f(x)的三条切线,求实数m的取值范围.
(1) ;(2)略;(3)
;(2)略;(3)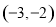 .
.
【解析】
试题分析:(1)利用导数与极值的关系可列出关于 的二元一次方程组,从而可求出函数的解析式.由题意可知
的二元一次方程组,从而可求出函数的解析式.由题意可知 ,依题意可知
,依题意可知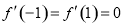 ,从而可列方程组
,从而可列方程组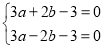 ,解得
,解得 ,所以函数
,所以函数 的解析式为
的解析式为 ;
;
(2)利用函数单调性求最值的方法,先判断函数 在区间
在区间 上的单调性,并求出函数
上的单调性,并求出函数 在区间
在区间 上的最大值与最小值之差,从而命题可得证明.由(1)可知
上的最大值与最小值之差,从而命题可得证明.由(1)可知 ,令
,令 ,解得
,解得 ,即函数
,即函数 在区间
在区间 上为单调递减,所以
上为单调递减,所以 ,
, ,因为对于区间
,因为对于区间 上的任意两个自变量的值
上的任意两个自变量的值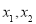 ,
,
都有 ,所以命题得证;
,所以命题得证;
(3)由(1)可知 , 由曲线方程
, 由曲线方程 可知点
可知点 不在曲线上.
不在曲线上.
设切点为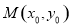 ,则
,则
因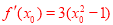 ,故切线的斜率为
,故切线的斜率为 ,整理得
,整理得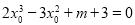 ,
,
因为过点 可作曲线的三条切线,所以关于
可作曲线的三条切线,所以关于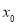 的方程
的方程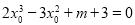 有三个实根,
有三个实根,
设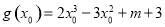 ,则
,则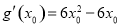 ,由
,由 ,得
,得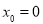 或
或 ,
,
所以 在
在 ,
,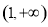 上单调递增,在
上单调递增,在 上单调递减,因此函数
上单调递减,因此函数 的极值点为0、1,
的极值点为0、1,
所以关于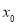 的方程
的方程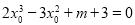 有三个实根的充要条件是
有三个实根的充要条件是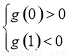 ,解得
,解得 .
.
故所求实数 的取值范围为
的取值范围为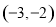 .
.
试题解析:(1)f′(x)=3ax2+2bx-3,依题意,f′(1)=f′(-1)=0,
即 解得a=1,b=0.∴f(x)=x3-3x.-------3分
解得a=1,b=0.∴f(x)=x3-3x.-------3分
(2)∵f(x)=x3-3x,∴f′(x)= 3x2-3=3(x+1)(x-1),
当-1<x<1时,f′(x)<0,故f(x)在区间[-1, 1]上为减函数,fmax(x)=f(-1)=2,fmin(x)=f(1)=-2
∵对于区间[-1,1]上任意两个自变量的值x1,x2,
都有|f(x1)-f(x2)|≤|fmax(x) -fmin(x)|,所以|f(x1)-f(x2)|≤2-(-2)=4 -----7分
(3)f′(x)=3x2-3=3(x+1)(x-1),
∵曲线方程为y=x3-3x,∴点A(1,m)不在曲线上.
设切点为M(x0,y0),则点M的坐标满足 因
因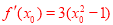 ,
,
故切线的斜率为 ,整理得
,整理得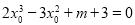 ,
,
因为过点 可作曲线的三条切线,所以关于
可作曲线的三条切线,所以关于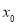 的方程
的方程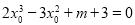 有三个实根,
有三个实根,
设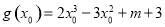 ,则
,则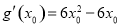 ,由
,由 ,得
,得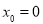 或
或 ,
,
所以 在
在 ,
,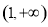 上单调递增,在
上单调递增,在 上单调递减,因此函数
上单调递减,因此函数 的极值点为0、1,
的极值点为0、1,
所以关于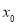 的方程
的方程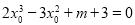 有三个实根的充要条件是
有三个实根的充要条件是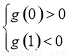 ,解得
,解得 .
.
故所求实数 的取值范围为
的取值范围为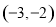 . 12分
. 12分
考点:1.导函数的应用;2.利用函数最值证明不等式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| A、?x0∈R,log2x0>0 | B、?x0∈R,log2x0≥0 | C、?x∈R,log2x≥0 | D、?x∈R,log2x>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、484种 | B、552种 | C、560种 | D、612种 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 | 3 | 4 |
| 4 | 3 | 1 | 2 |
| 2 | 1 | 4 | 3 |
| 3 | 4 | 2 | 1 |
| A、432 | B、576 |
| C、720 | D、864 |
查看答案和解析>>
科目:高中数学 来源:2015届西藏拉萨中学高三第三次月考理科数学试卷(解析版) 题型:解答题
(本题满分12分)已知函数 ,x∈R.(其中m为常数).
,x∈R.(其中m为常数).
(1)当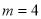 时,求函数的极值点和极值;
时,求函数的极值点和极值;
(2)若函数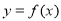 在区间(0,+∞)上有两个极值点,求实数
在区间(0,+∞)上有两个极值点,求实数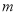 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com