
| A. | $\frac{8}{81}$ | B. | $\frac{16}{81}$ | C. | $\frac{32}{81}$ | D. | $\frac{64}{81}$ |
分析 设出正方体的棱长,求出球的半径,然后求解球的内接正四棱锥的体积的表达式,求出正四棱锥体积的最大值,即可求解K.
解答 解:设正方体的棱长为2,则正方体的内切球的半径为1,正方体的体积V2=8.
设正四棱锥底面边长为a,底面到球心的距离为x,
则:x2+($\frac{\sqrt{2}a}{2}$)2=12,
是正四棱锥的体积为:V=$\frac{1}{3}$a2h=$\frac{1}{3}$a2(1+x)=$\frac{2}{3}$(1-x2)(1+x)其中x(0,1),
因为$\frac{2}{3}$(1-x2)(1+x)=$\frac{1}{3}$(2-2x)(1+x)(1+x)≤$\frac{1}{3}$$({\frac{2-2x+1+x+1+x}{3})}^{3}$=$\frac{64}{81}$,当且仅当x=$\frac{1}{3}$时取等号.
正四棱锥的最大值为:$\frac{64}{81}$,即V1=$\frac{64}{81}$,V1=KV2
可得$\frac{64}{81}$=8k,解得k=$\frac{8}{81}$.
故选:A.
点评 本题考查正方体的内接球,球的内接体,几何体的体积的求法,基本不等式的应用,考查分析问题解决问题以及空间想象能力计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届云南曲靖市高三上半月考一数学试卷(解析版) 题型:填空题
已知函数 ,若
,若 是从
是从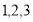 三个数中任取的一个数,
三个数中任取的一个数, 是从
是从 三个数中任取的一个数,则使函数
三个数中任取的一个数,则使函数 有极值点的概率为_______.
有极值点的概率为_______.
查看答案和解析>>
科目:高中数学 来源:2017届四川成都七中高三10月段测数学(文)试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
在直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数,
为参数,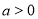 ),在以坐标原点为极点,
),在以坐标原点为极点, 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线 .
.
(1)求曲线 的普通方程,并将
的普通方程,并将 的方程化为极坐标方程;
的方程化为极坐标方程;
(2)直线 的极坐标方程为
的极坐标方程为 ,其中
,其中 满足
满足 ,若曲线
,若曲线 与
与 的公共点都在
的公共点都在 上,求
上,求 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\sqrt{2}$)∪[$\sqrt{2}$,+∞) | B. | [-2,2] | C. | [-2,-$\sqrt{2}$]∪[$\sqrt{2}$,2] | D. | [-$\sqrt{2}$,$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在圆内接四边形ABCD中,AB∥DC,过点A作圆的切线与CB的延长线交于点E.若AB=AD=BC=5,AE=6,则BE=4DC=$\frac{25}{4}$.
如图,在圆内接四边形ABCD中,AB∥DC,过点A作圆的切线与CB的延长线交于点E.若AB=AD=BC=5,AE=6,则BE=4DC=$\frac{25}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com