如图①所示，四边形
为等腰梯形，
，且
于点
为
的中点．将
沿着
折起至
的位置，得到如图②所示的四棱锥
.
（1）求证：
平面
；
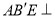（2）若平面
平面
，求二面角
的余弦值．
学练快车道快乐假期寒假作业系列答案科目：高中数学 来源：2017届福建福州外国语学校高三适应性考试四数学（理）试卷（解析版） 题型：填空题
在一项田径比赛中，甲、乙、丙三人的夺冠呼声最高．观众
做了一项预测：
说：“我认为冠军不会是甲，也不会是乙”．
说：“我觉得冠军不会是甲，冠军会是丙”．
说：“我认为冠军不会是丙，而是甲”．
比赛结果出来后，发现三人中有一人的两个判断都对，一人的两个判断都错，还有一人的两个判断一对一错，根据以上情况可判断冠军是__________．
查看答案和解析>>
科目：高中数学 来源：2017届河南新乡市高三上学期第一次调研数学（文）试卷（解析版） 题型：解答题
选修4-4：坐标系与参数方程
在直角坐标系
中，以
为极点，
轴的正半轴为极轴建立极坐标系，已知直线
的参数方程为
，（
为参数），曲线
的普通方程为
，点
的极坐标为
．
（1）求直线
的普通方程和曲线
的极坐标方程；
（2）若将直线
向右平移2个单位得到直线
，设与
相交于
两点，求
的面积．
查看答案和解析>>
科目：高中数学 来源：2017届河南新乡市高三上学期第一次调研数学（文）试卷（解析版） 题型：选择题
已知各项均不为0的等差数列
满足
，数列
为等比数列，且
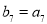，则
（ ）
A．16 B．8
C．4 D．25
查看答案和解析>>
科目：高中数学 来源：2017届河南新乡市高三上学期第一次调研数学（理）试卷（解析版） 题型：解答题
选修4-4：坐标系与参数方程
在直角坐标系
中，以
为极点，
轴的正半轴为极轴建立极坐标系，已知直线
的参数方程为
，（
为参数），曲线
的普通方程为
，点
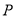的极坐标为
．
（1）求直线
的普通方程和曲线
的极坐标方程；
（2）若将直线
向右平移2个单位得到直线
，设与
相交于
两点，求
的面积．
查看答案和解析>>
科目：高中数学 来源：2017届河南新乡市高三上学期第一次调研数学（理）试卷（解析版） 题型：选择题
已知各项均不为0的等差数列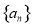
满足
，数列
为等比数列，且
，则
（ ）
A．25 B．16
C．8 D．4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，若
间的夹角为
，则
____________．
B．
D．
是锐角，则
的最小值是_____．