
设椭圆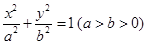 的左右顶点分别为
的左右顶点分别为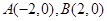 ,离心率
,离心率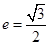 .过该椭圆上任一点P作PQ⊥x轴,垂足为Q,点C在QP的延长线上,且
.过该椭圆上任一点P作PQ⊥x轴,垂足为Q,点C在QP的延长线上,且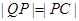 .
.
(1)求椭圆的方程;
(2)求动点C的轨迹E的方程;
(3)设直线AC(C点不同于A,B)与直线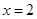 交于点R,D为线段RB的中点,试判断直线CD与曲线E的位置关系,并证明你的结论.
交于点R,D为线段RB的中点,试判断直线CD与曲线E的位置关系,并证明你的结论.
(1)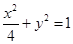 ;(2)
;(2)  ;(3)
直线
;(3)
直线 与圆
与圆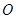 相切,证明见解析.
相切,证明见解析.
【解析】
试题分析:(1)要求椭圆的方程,就要知道a,b,由点A知道a=2,由离心率可求得c,由a2=b2+c2进而求出b=1;(2)求动点的轨迹方程,首先设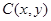 ,
,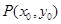 ,利用
,利用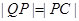 用C点表示P点坐标,
用C点表示P点坐标,  ,代入椭圆方程,从而得到动点C的轨迹;(3)直线与圆的位置关系有三种,相交,相切,相离,判断的方法是圆心到直线的距离与半径的关系,如果⊙O的半径为r,圆心O到直线l的距离为d,那么:直线l与⊙O相交
,代入椭圆方程,从而得到动点C的轨迹;(3)直线与圆的位置关系有三种,相交,相切,相离,判断的方法是圆心到直线的距离与半径的关系,如果⊙O的半径为r,圆心O到直线l的距离为d,那么:直线l与⊙O相交 d<r;直线l与⊙O相切
d<r;直线l与⊙O相切 d=r;直线l与⊙O相离
d=r;直线l与⊙O相离 d>r;求出圆心到直线的距离后和半径进行比较,可得直线与圆的位置关系.
d>r;求出圆心到直线的距离后和半径进行比较,可得直线与圆的位置关系.
试题解析:(1)由题意可得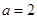 ,
,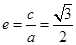 ,
,
∴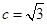 ,
,
∴ ,
,
∴椭圆的方程为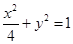 .
.
(2)设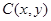 ,
,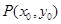 ,由题意得
,由题意得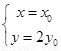 ,即
,即 ,
,
又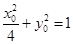 ,代入得
,代入得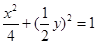 ,即
,即 .
.
即动点 的轨迹
的轨迹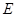 的方程为
的方程为 .
.
(3)设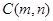 ,点
,点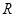 的坐标为
的坐标为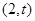 ,
,
∵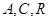 三点共线,
三点共线,
∴ ,
,
而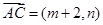 ,
,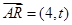 ,
,
则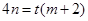 ,
,
∴ ,
,
∴点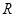 的坐标为
的坐标为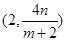 ,点
,点 的坐标为
的坐标为 ,
,
∴直线 的斜率为
的斜率为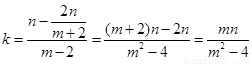 ,
,
而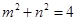 ,
,
∴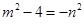 ,
,
∴ ,
,
∴直线 的方程为
的方程为 ,
,
化简得 ,
,
∴圆心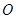 到直线
到直线 的距离
的距离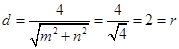 ,
,
∴直线 与圆
与圆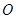 相切.
相切.
考点:1.椭圆;2.动点轨迹;3.直线与圆的位置关系.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2013-2014学年河南省南阳市高三第三次联考(高考模拟)理科数学试卷(解析版) 题型:解答题
已知圆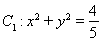 ,直线
,直线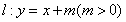 与圆
与圆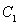 相切,且交椭圆
相切,且交椭圆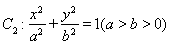 于
于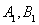 两点,c是椭圆的半焦距,
两点,c是椭圆的半焦距,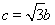
(1)求m的值;
(2)O为坐标原点,若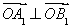 ,求椭圆
,求椭圆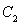 的方程;
的方程;
(3)在(2)的条件下,设椭圆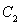 的左右顶点分别为A,B,动点
的左右顶点分别为A,B,动点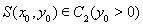 ,直线
,直线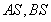 与直线
与直线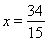 分别交于M,N两点,求线段MN的长度的最小值
分别交于M,N两点,求线段MN的长度的最小值
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河南省南阳市高三第三次联考(高考模拟)文科数学试卷(解析版) 题型:解答题
已知圆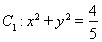 ,直线
,直线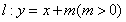 与圆
与圆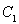 相切,且交椭圆
相切,且交椭圆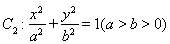 于
于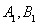 两点,c是椭圆的半焦距,
两点,c是椭圆的半焦距,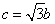 .
.
(1)求m的值;
(2)O为坐标原点,若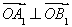 ,求椭圆
,求椭圆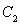 的方程;
的方程;
(3)在(2)的条件下,设椭圆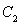 的左右顶点分别为A,B,动点
的左右顶点分别为A,B,动点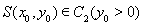 ,直线
,直线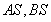 与直线
与直线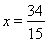 分别交于M,N两点,求线段MN的长度的最小值.
分别交于M,N两点,求线段MN的长度的最小值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西南昌市高三第二次模拟测试文科数学试卷(解析版) 题型:解答题
已知椭圆C: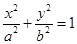 的离心率等于
的离心率等于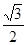 ,点P
,点P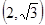 在椭圆上。
在椭圆上。
(1)求椭圆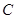 的方程;
的方程;
(2)设椭圆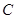 的左右顶点分别为
的左右顶点分别为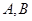 ,过点
,过点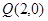 的动直线
的动直线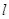 与椭圆
与椭圆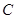 相交于
相交于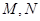 两点,是否存在定直线
两点,是否存在定直线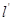 :
: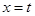 ,使得
,使得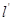 与
与 的交点
的交点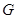 总在直线
总在直线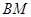 上?若存在,求出一个满足条件的
上?若存在,求出一个满足条件的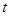 值;若不存在,说明理由.
值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山西省高三下学期5月月考理科数学试卷(解析版) 题型:解答题
已知椭圆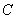 :
: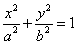 的离心率等于
的离心率等于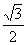 ,点
,点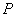
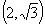 在椭圆上.
在椭圆上.
(I)求椭圆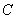 的方程;
的方程;
(Ⅱ)设椭圆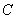 的左右顶点分别为
的左右顶点分别为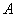 ,
,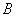 ,过点
,过点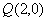 的动直线
的动直线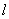 与椭圆
与椭圆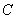 相交于
相交于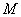 ,
,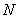 两点,是否存在定直线
两点,是否存在定直线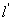 :
: ,使得
,使得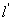 与
与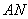 的交点
的交点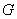 总在直线
总在直线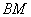 上?若存在,求出一个满足条件的
上?若存在,求出一个满足条件的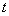 值;若不存在,说明理由。
值;若不存在,说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com