【答案】
分析:若(1)(2)→甲,由(1)利用平方差及完全平方公式变形得到关于a,b及c的关系式,利用余弦定理表示出cosC,把得到的关系式代入求出cosC的值,由C为三角形的内角,利用特殊角的三角函数值求出C为60°,再利用诱导公式及两角和与差的正弦函数公式化简(2)中的等式,得到sin(B-C)=0,由B和C为三角形的内角,得到B-C的范围,利用特殊角的三角函数值得到B=C,从而得到三角形为等边三角形;
若(2)(4)→乙,利用诱导公式及两角和与差的正弦函数公式化简(2)中的等式,得到sin(B-C)=0,由B和C为三角形的内角,得到B-C的范围,利用特殊角的三角函数值得到B=C,再利用正弦定理化简(4)中的等式,得到a=
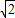
b,利用勾股定理的逆定理得到∠A为直角,从而得到三角形为等腰直角三角形;
若(3)(4)→乙,利用正弦定理化简(4)中的等式,得到a=
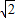
b,利用勾股定理的逆定理得到∠A为直角,再利用正弦定理化简(3)中的两等式,分别表示出sinA,两者相等再利用二倍角的正弦函数公式,得到sin2B=sin2C,由B和C都为三角形的内角,可得B=C,从而得到三角形为等腰直角三角形.三者选择一个即可.
解答:解:由(1)(2)为条件,甲为结论,得到的命题为真命题,理由如下:
证明:由(a+b+c)(a+b-c)=3ab,变形得:
a
2+b
2+2ab-c
2=3ab,即a
2+b
2-c
2=ab,
则cosC=
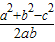
=

,又C为三角形的内角,
∴C=60°,
又sinA=sin(B+C)=sinBcosC+cosBsinC=2cosBsinC,
即sinBcosC-cosBsinC=sin(B-C)=0,
∵-π<B-C<π,
∴B-C=0,即B=C,
则A=B=C=60°,
∴△ABC是等边三角形;
以(2)(4)作为条件,乙为结论,得到的命题为真命题,理由为:
证明:化简得:sinA=sin(B+C)=sinBcosC+cosBsinC=2cosBsinC,
即sinBcosC-cosBsinC=sin(B-C)=0,
∵-π<B-C<π,
∴B-C=0,即B=C,
∴b=c,
由正弦定理
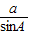
=
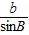
=
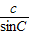
=2R得:
sinA=
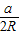
,sinB=
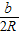
,sinC=
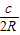
,
代入
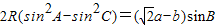
得:
2R•(
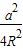
-
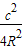
)=(
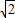
a-b)•
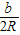
,
整理得:a
2-b
2=
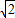
ab-b
2,即a
2=
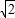
ab,
∴a=
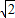
b,
∴a
2=2b
2,又b
2+c
2=2b
2,
∴a
2=b
2+c
2,
∴∠A=90°,
则三角形为等腰直角三角形;
以(3)(4)作为条件,乙为结论,得到的命题为真命题,理由为:
证明:由正弦定理
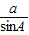
=
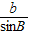
=
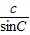
=2R得:
sinA=
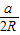
,sinB=
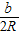
,sinC=

,
代入
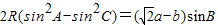
得:
2R•(
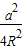
-
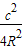
)=(
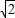
a-b)•
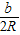
,
整理得:a
2-b
2=
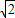
ab-b
2,即a
2=
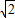
ab,
∴a=
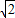
b,
∴a
2=2b
2,又b
2+c
2=2b
2,
∴a
2=b
2+c
2,
∴∠A=90°,
又b=acosC,c=acosB,
根据正弦定理得:sinB=sinAcosC,sinC=sinAcosB,
∴
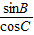
=
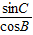
,即sinBcosB=sinCcosC,
∴sin2B=sin2C,又B和C都为三角形的内角,
∴2B=2C,即B=C,
则三角形为等腰直角三角形.
故答案为:(1)(2)→甲 或 (2)(4)→乙 或 (3)(4)→乙
点评:此题考查了三角形形状的判断,涉及的知识有正弦、余弦定理,两角和与差的正弦函数公式,勾股定理,等边三角形的判定,等腰三角形的判定与性质,属于条件开放型题,是一类背景新、解题活、综合性强、无现成模式的题型.解答此类题需要运用观察、类比、猜测、归纳、推理等多种探索活动寻求解题策略.

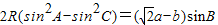
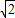 b,利用勾股定理的逆定理得到∠A为直角,从而得到三角形为等腰直角三角形;
b,利用勾股定理的逆定理得到∠A为直角,从而得到三角形为等腰直角三角形;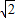 b,利用勾股定理的逆定理得到∠A为直角,再利用正弦定理化简(3)中的两等式,分别表示出sinA,两者相等再利用二倍角的正弦函数公式,得到sin2B=sin2C,由B和C都为三角形的内角,可得B=C,从而得到三角形为等腰直角三角形.三者选择一个即可.
b,利用勾股定理的逆定理得到∠A为直角,再利用正弦定理化简(3)中的两等式,分别表示出sinA,两者相等再利用二倍角的正弦函数公式,得到sin2B=sin2C,由B和C都为三角形的内角,可得B=C,从而得到三角形为等腰直角三角形.三者选择一个即可.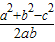 =
= ,又C为三角形的内角,
,又C为三角形的内角,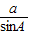 =
=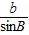 =
=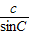 =2R得:
=2R得: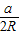 ,sinB=
,sinB=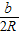 ,sinC=
,sinC=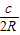 ,
,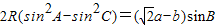 得:
得: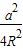 -
-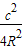 )=(
)=(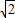 a-b)•
a-b)•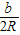 ,
,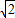 ab-b2,即a2=
ab-b2,即a2=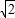 ab,
ab,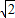 b,
b,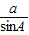 =
=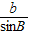 =
=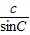 =2R得:
=2R得: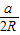 ,sinB=
,sinB=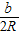 ,sinC=
,sinC= ,
,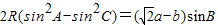 得:
得: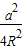 -
-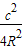 )=(
)=(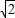 a-b)•
a-b)•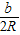 ,
,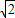 ab-b2,即a2=
ab-b2,即a2=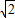 ab,
ab,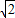 b,
b,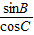 =
=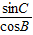 ,即sinBcosB=sinCcosC,
,即sinBcosB=sinCcosC,

 阅读快车系列答案
阅读快车系列答案