
函数 .
.
(1)若 ,函数
,函数 在区间
在区间 上是单调递增函数,求实数
上是单调递增函数,求实数 的取值范围;
的取值范围;
(2)设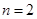 ,若对任意
,若对任意 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(1)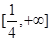 ;(2)
;(2)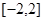 .
.
解析试题分析:(1)由题意可得,当 时,
时, 在区间
在区间 上是单调递增函数等价于对于任意的
上是单调递增函数等价于对于任意的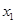 ,
,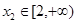 (不妨
(不妨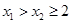 ),
),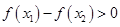 恒成立,从而将问题转化为
恒成立,从而将问题转化为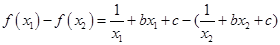
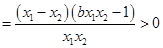 在
在 恒成立,即有
恒成立,即有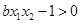 ,
,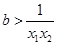 在
在 上恒成立,而的
上恒成立,而的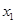 ,
,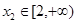 ,且
,且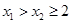 ,故有
,故有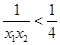 ,因此分析可得要使
,因此分析可得要使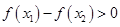 恒成立,只需
恒成立,只需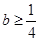 ,即有实数
,即有实数 的取值范围是
的取值范围是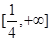 ;(2)由题意分析可得问题等价于在
;(2)由题意分析可得问题等价于在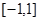 上,
上,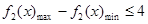 ,从而可将问题转化为在
,从而可将问题转化为在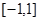 上,求二次函数
上,求二次函数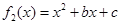 的最大值与最小值,因此需要对二次函数的对称轴
的最大值与最小值,因此需要对二次函数的对称轴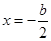 分以下四种情况讨论:①当
分以下四种情况讨论:①当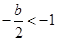 ,即
,即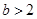 ;②当
;②当 ,即
,即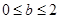 ;③当
;③当 ,即
,即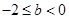 ;④当
;④当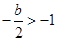 ,即
,即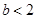 ,结合二次函数的图像和性质,可分别得到
,结合二次函数的图像和性质,可分别得到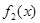 在以上四种情况下的最大值与最小值,从而可得实数
在以上四种情况下的最大值与最小值,从而可得实数 的取值范围是
的取值范围是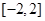 .
.
试题解析:(1) 时,
时,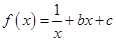 ,
,
任设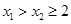 ,
,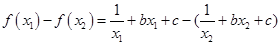
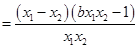 , ..2分
, ..2分 ,
,
∵函数 在
在 上是单调递增函数,∴恒有
上是单调递增函数,∴恒有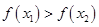 ,..........3分
,..........3分
∴恒有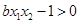 ,即恒有
,即恒有 , .4分
, .4分
当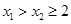 时,
时,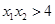 ,∴
,∴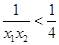 ,∴
,∴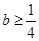 ,即实数
,即实数 的取值范围是
的取值范围是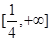 ..6分
..6分
(2)当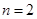 时
时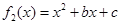 ,
,
对任意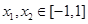 有
有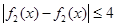 恒成立等价于
恒成立等价于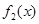 在
在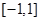 上的最大值与最小值之差
上的最大值与最小值之差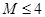 ..7分
..7分
当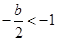 ,即
,即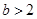 时,
时,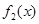 在
在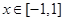 上单调递增,
上单调递增,
∴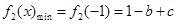 ,
,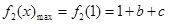 ,∴
,∴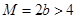 ,与题设矛盾; ..9分
,与题设矛盾; ..9分
当 ,即
,即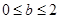


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
用水清洗一堆蔬菜上残留的农药,对用一定量的水清洗一次的效果作如下假定:用一个单位的水可洗掉蔬菜上残留农药的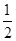 ,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用
,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用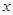 单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数
单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数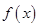 .
.
⑴试规定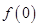 的值,并解释其实际意义;
的值,并解释其实际意义;
⑵试根据假定写出函数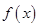 应满足的条件和具有的性质;
应满足的条件和具有的性质;
⑶设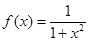 ,现有
,现有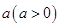 单位量的水,可以清洗一次,也可以把水平均分成两份后清洗两次.试问用那种方案清洗后蔬菜上残留的农药量比较少?说明理由.
单位量的水,可以清洗一次,也可以把水平均分成两份后清洗两次.试问用那种方案清洗后蔬菜上残留的农药量比较少?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某渔业公司年初用49万元购买一艘捕鱼船,第一年各种费用6万元,以后每年都增加2万元,每年捕鱼收益25万元.
(1)问第几年开始获利?
(2)若干年后,有两种处理方案:①年平均获利最大时,以18万元出售该渔船;②总纯收入获利最大时,以9万元出售该渔船.问哪种方案最合算?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设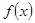 是定义在
是定义在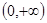 上的函数,且
上的函数,且 ,对任意
,对任意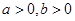 ,若经过点
,若经过点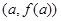 ,
,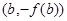 的直线与
的直线与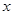 轴的交点为
轴的交点为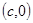 ,则称
,则称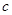 为
为 关于函数
关于函数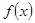 的平均数,记为
的平均数,记为 ,例如,当
,例如,当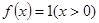 时,可得
时,可得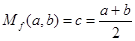 ,即
,即 为
为 的算术平均数.
的算术平均数.
当 时,
时, 为
为 的几何平均数;
的几何平均数;
当 时,
时, 为
为 的调和平均数
的调和平均数 ;
;
(以上两空各只需写出一个符合要求的函数即可)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2014·郑州模拟)已知函数f(x)=ex+ax,g(x)=ax-lnx,其中a≤0.
(1)求f(x)的极值.
(2)若存在区间M,使f(x)和g(x)在区间M上具有相同的单调性,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com