
设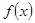 是定义在
是定义在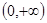 上的函数,且
上的函数,且 ,对任意
,对任意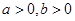 ,若经过点
,若经过点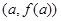 ,
,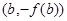 的直线与
的直线与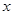 轴的交点为
轴的交点为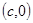 ,则称
,则称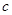 为
为 关于函数
关于函数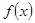 的平均数,记为
的平均数,记为 ,例如,当
,例如,当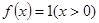 时,可得
时,可得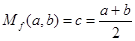 ,即
,即 为
为 的算术平均数.
的算术平均数.
当 时,
时, 为
为 的几何平均数;
的几何平均数;
当 时,
时, 为
为 的调和平均数
的调和平均数 ;
;
(以上两空各只需写出一个符合要求的函数即可)
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:填空题
已知定义在 上的偶函数
上的偶函数 满足:
满足: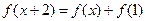 且在区间
且在区间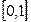 上
上
单调递增,那么,下列关于此函数 性质的表述:
性质的表述:
①函数 的图象关于直线
的图象关于直线 对称; ②函数
对称; ②函数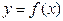 是周期函数;
是周期函数;
③当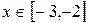 时,
时, ; ④函数
; ④函数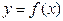 的图象上横坐标为偶数的点都是函数的极小值点。 其中正确表述的番号是 .
的图象上横坐标为偶数的点都是函数的极小值点。 其中正确表述的番号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对于函数 ,若存在实数对(
,若存在实数对( ),使得等式
),使得等式 对定义域中的每一个
对定义域中的每一个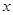 都成立,则称函数
都成立,则称函数 是“(
是“( )型函数”.
)型函数”.
(1) 判断函数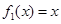 是否为 “(
是否为 “( )型函数”,并说明理由;
)型函数”,并说明理由;
(2) 若函数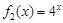 是“(
是“( )型函数”,求出满足条件的一组实数对
)型函数”,求出满足条件的一组实数对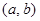 ;
;
(3)已知函数 是“
是“ 型函数”,对应的实数对
型函数”,对应的实数对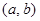 为
为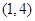 ,当
,当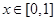 时,
时,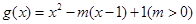 ,若当
,若当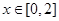 时,都有
时,都有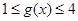 ,试求
,试求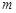 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知定义域为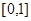 的函数
的函数 同时满足以下三个条件:
同时满足以下三个条件:
①对任意的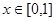 ,总有
,总有 ;
;
②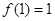 ;
;
③当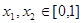 ,且
,且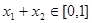 时,
时,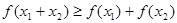 成立.
成立.
称这样的函数为“友谊函数”.
请解答下列各题:
(1)已知 为“友谊函数”,求
为“友谊函数”,求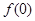 的值;
的值;
(2)函数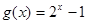 在区间
在区间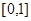 上是否为“友谊函数”?请给出理由;
上是否为“友谊函数”?请给出理由;
(3)已知 为“友谊函数”,假定存在
为“友谊函数”,假定存在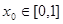 ,使得
,使得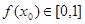 ,且
,且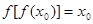 ,求证:
,求证: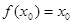 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某公司为一家制冷设备厂设计生产一种长方形薄板,其周长为4米,这种薄板须沿其对角线折叠后使用.如图所示,ABCD(AB>AD)为长方形薄板,沿AC折叠后,AB′交DC于点P.当△ADP的面积最大时最节能,凹多边形ACB′PD的面积最大时制冷效果最好.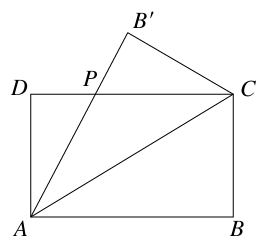
(1)设AB=x(米),用x表示图中DP的长度,并写出x的取值范围;
(2)若要求最节能,应怎样设计薄板的长和宽?
(3)若要求制冷效果最好,应怎样设计薄板的长和宽?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com