
对于函数 ,若存在实数对(
,若存在实数对( ),使得等式
),使得等式 对定义域中的每一个
对定义域中的每一个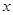 都成立,则称函数
都成立,则称函数 是“(
是“( )型函数”.
)型函数”.
(1) 判断函数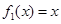 是否为 “(
是否为 “( )型函数”,并说明理由;
)型函数”,并说明理由;
(2) 若函数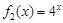 是“(
是“( )型函数”,求出满足条件的一组实数对
)型函数”,求出满足条件的一组实数对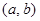 ;
;
(3)已知函数 是“
是“ 型函数”,对应的实数对
型函数”,对应的实数对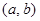 为
为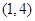 ,当
,当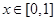 时,
时,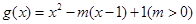 ,若当
,若当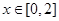 时,都有
时,都有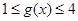 ,试求
,试求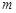 的取值范围.
的取值范围.
(1)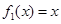 不是“
不是“ 型函数”,理由详见解析;(2)
型函数”,理由详见解析;(2)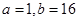 (满足
(满足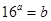 的实数对
的实数对 均是正确答案);(3)
均是正确答案);(3)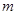 的取值范围是
的取值范围是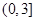 .
.
解析试题分析:(1)根据条件中的描述,若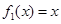 是“
是“ 型函数”,则需存在实数
型函数”,则需存在实数 ,使得
,使得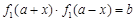 对于任意
对于任意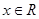 都成立,即
都成立,即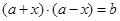 ,
,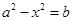 对任意
对任意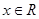 都成立,这显然是不可能的,因此假设不成立,即
都成立,这显然是不可能的,因此假设不成立,即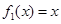 不是“
不是“ 型函数”;(2)根据条件描述,
型函数”;(2)根据条件描述,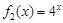 是“
是“ 型函数”需存在实数对
型函数”需存在实数对 ,使得
,使得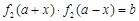 对于任意
对于任意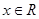 都成立,即
都成立,即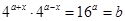 对任意
对任意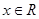 均成立,故所取的实数对只需满足等式
均成立,故所取的实数对只需满足等式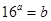 即可,例如
即可,例如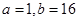 ;
;
(3)根据 是“
是“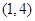 型函数”可知:
型函数”可知: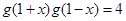 ,即
,即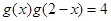 ,而当
,而当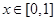 时,
时,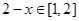 ,故当
,故当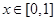 时,若有
时,若有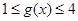 ,必有当
,必有当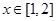 时,
时,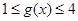 ,因此要使当
,因此要使当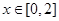 时,都有
时,都有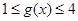 即等价于当
即等价于当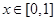 时,
时,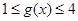 恒成立,因此可以得到不等式
恒成立,因此可以得到不等式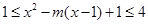 在
在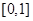 上恒成立,若
上恒成立,若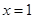 :显然不等式在
:显然不等式在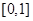 上成立,若
上成立,若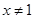 :参变分离后可转化为转化为
:参变分离后可转化为转化为 ,显然,当
,显然,当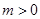 时,不等式(1)成立,而要使不等式(2)成立,
时,不等式(1)成立,而要使不等式(2)成立,
只需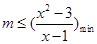 ,通过构造函数令
,通过构造函数令 及
及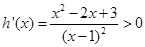 ,可知
,可知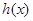 在
在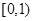 上单调递增,故
上单调递增,故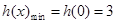 ,因此只需
,因此只需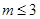 即可从而得到实数
即可从而得到实数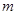 的取值范围是
的取值范围是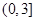 .
.
试题解析:(1)假设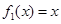 是“(
是“( )型函数”,则由题意存在实数对
)型函数”,则由题意存在实数对 ,使得
,使得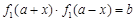 对于任意
对于任意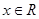 都成立,即
都成立,即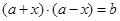 ,
,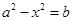 对任意
对任意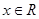 都成立,这显然是不可能的,因此假设不成立,即
都成立,这显然是不可能的,因此假设不成立,即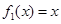 不是
不是

 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:解答题
某人准备租一辆车从孝感出发去武汉,已知从出发点到目的地的距离为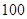
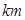 ,按交通法规定:这段公路车速限制在
,按交通法规定:这段公路车速限制在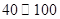 (单位:
(单位: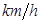 )之间.假设目前油价为
)之间.假设目前油价为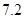 (单位:元
(单位:元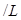 ),汽车的耗油率为
),汽车的耗油率为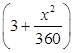 (单位:
(单位: ), 其中
), 其中 (单位:
(单位: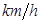 )为汽车的行驶速度,耗油率指汽车每小时的耗油量.租车需付给司机每小时的工资为
)为汽车的行驶速度,耗油率指汽车每小时的耗油量.租车需付给司机每小时的工资为 元,不考虑其它费用,这次租车的总费用最少是多少?此时的车速
元,不考虑其它费用,这次租车的总费用最少是多少?此时的车速 是多少?(注:租车总费用=耗油费+司机的工资)
是多少?(注:租车总费用=耗油费+司机的工资)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
用水清洗一堆蔬菜上残留的农药,对用一定量的水清洗一次的效果作如下假定:用一个单位的水可洗掉蔬菜上残留农药的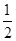 ,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用
,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用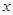 单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数
单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数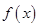 .
.
⑴试规定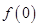 的值,并解释其实际意义;
的值,并解释其实际意义;
⑵试根据假定写出函数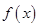 应满足的条件和具有的性质;
应满足的条件和具有的性质;
⑶设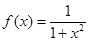 ,现有
,现有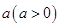 单位量的水,可以清洗一次,也可以把水平均分成两份后清洗两次.试问用那种方案清洗后蔬菜上残留的农药量比较少?说明理由.
单位量的水,可以清洗一次,也可以把水平均分成两份后清洗两次.试问用那种方案清洗后蔬菜上残留的农药量比较少?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两个工厂,甲厂位于一直线河岸的岸边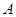 处,乙厂与甲厂在河的同侧,乙厂位于离河岸40千米的
处,乙厂与甲厂在河的同侧,乙厂位于离河岸40千米的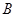 处,乙厂到河岸的垂足
处,乙厂到河岸的垂足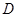 与
与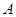 相距50千米,两厂要在此岸边
相距50千米,两厂要在此岸边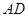 之间合建一个供水站
之间合建一个供水站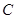 ,从供水站到甲厂和乙厂的水管费用分别为每千米3
,从供水站到甲厂和乙厂的水管费用分别为每千米3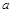 元和5
元和5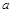 元,若
元,若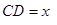 千米,设总的水管费用为
千米,设总的水管费用为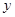 元,如图所示,
元,如图所示,
(1)写出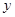 关于
关于 的函数表达式;
的函数表达式;
(2)问供水站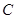 建在岸边何处才能使水管费用最省?
建在岸边何处才能使水管费用最省? 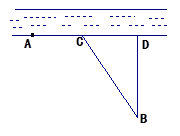
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某渔业公司年初用49万元购买一艘捕鱼船,第一年各种费用6万元,以后每年都增加2万元,每年捕鱼收益25万元.
(1)问第几年开始获利?
(2)若干年后,有两种处理方案:①年平均获利最大时,以18万元出售该渔船;②总纯收入获利最大时,以9万元出售该渔船.问哪种方案最合算?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设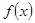 是定义在
是定义在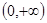 上的函数,且
上的函数,且 ,对任意
,对任意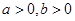 ,若经过点
,若经过点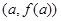 ,
,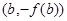 的直线与
的直线与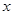 轴的交点为
轴的交点为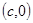 ,则称
,则称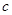 为
为 关于函数
关于函数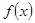 的平均数,记为
的平均数,记为 ,例如,当
,例如,当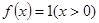 时,可得
时,可得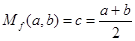 ,即
,即 为
为 的算术平均数.
的算术平均数.
当 时,
时, 为
为 的几何平均数;
的几何平均数;
当 时,
时, 为
为 的调和平均数
的调和平均数 ;
;
(以上两空各只需写出一个符合要求的函数即可)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分)本题共有2个小题,第1小题满分6分,第2个小题满分8分。
某加油站拟造如图所示的铁皮储油罐(不计厚度,长度单位:米),其中储油罐的中间为圆柱形,左右两端均为半球形,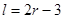 (
(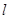 为圆柱的高,
为圆柱的高,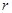 为球的半径,
为球的半径,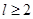 ).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为
).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为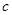 千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为
千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为 千元.
千元.
(1)写出 关于
关于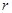 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(2)求该储油罐的建造费用最小时的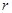 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com