
甲、乙两个工厂,甲厂位于一直线河岸的岸边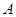 处,乙厂与甲厂在河的同侧,乙厂位于离河岸40千米的
处,乙厂与甲厂在河的同侧,乙厂位于离河岸40千米的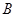 处,乙厂到河岸的垂足
处,乙厂到河岸的垂足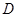 与
与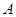 相距50千米,两厂要在此岸边
相距50千米,两厂要在此岸边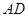 之间合建一个供水站
之间合建一个供水站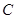 ,从供水站到甲厂和乙厂的水管费用分别为每千米3
,从供水站到甲厂和乙厂的水管费用分别为每千米3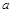 元和5
元和5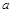 元,若
元,若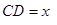 千米,设总的水管费用为
千米,设总的水管费用为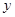 元,如图所示,
元,如图所示,
(1)写出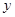 关于
关于 的函数表达式;
的函数表达式;
(2)问供水站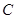 建在岸边何处才能使水管费用最省?
建在岸边何处才能使水管费用最省? 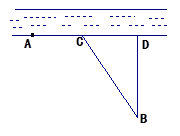
(1)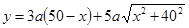 ,(2)A、D之间距甲厂20 km处
,(2)A、D之间距甲厂20 km处
解析试题分析:(1)由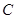 点的位置即可算出到甲、乙两厂的距离,得出距离后总的水管费用即可算出。(II)水管费用最省,即求(1)式中
点的位置即可算出到甲、乙两厂的距离,得出距离后总的水管费用即可算出。(II)水管费用最省,即求(1)式中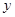 的最小值,利用求导数判断函数的单调性即可得出结果。
的最小值,利用求导数判断函数的单调性即可得出结果。
试题解析:(1)∵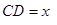 ,BD=40,AC=50-
,BD=40,AC=50- ,∴BC=
,∴BC=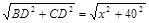
又总的水管费用为y元,依题意有: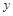 =3
=3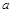 (50-x)+5
(50-x)+5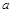
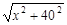
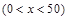 6分
6分
(2)由(1)得y′=-3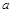 +
+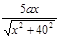 ,令y′=0,解得
,令y′=0,解得 =30 8分
=30 8分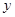 在(0,30)单调递减,在(30,50)单调递增上, 11分
在(0,30)单调递减,在(30,50)单调递增上, 11分
函数在 =30(km)处取得最小值,此时AC=50-
=30(km)处取得最小值,此时AC=50- ="20(km)" 13分
="20(km)" 13分
∴供水站建在A、D之间距甲厂20 km处,可使水管费用最省. 14分
考点:函数的应用题及函数的单调性


科目:高中数学 来源: 题型:解答题
经英国相关机构判断,MH370在南印度洋海域消失.中国两舰艇随即在边长为100海里的某正方形ABCD(如图)海域内展开搜索.两艘搜救船在A处同时出发,沿直线AP、AQ向前联合搜索,且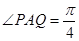 (其中点P、Q分别在边BC、CD上),搜索区域为平面四边形APCQ围成的海平面.设
(其中点P、Q分别在边BC、CD上),搜索区域为平面四边形APCQ围成的海平面.设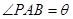 ,搜索区域的面积为
,搜索区域的面积为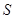 .
.
(1)试建立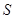 与
与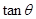 的关系式,并指出
的关系式,并指出 的取值范围;
的取值范围;
(2)求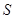 的最大值,并求此时
的最大值,并求此时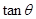 的值.
的值.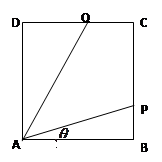
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,n台机器人M1,M2,……,Mn位于一条直线上,检测台M在线段M1 Mn上,n台机器人需把各自生产的零件送交M处进行检测,送检程序设定:当Mi把零件送达M处时,Mi+1即刻自动出发送检(i=1,2,……,n-1)已知Mi的送检速度为V(V>0), 且 记
记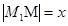 ,n台机器人送检时间总和为f(x).
,n台机器人送检时间总和为f(x).
 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对于函数 ,若存在实数对(
,若存在实数对( ),使得等式
),使得等式 对定义域中的每一个
对定义域中的每一个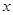 都成立,则称函数
都成立,则称函数 是“(
是“( )型函数”.
)型函数”.
(1) 判断函数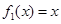 是否为 “(
是否为 “( )型函数”,并说明理由;
)型函数”,并说明理由;
(2) 若函数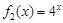 是“(
是“( )型函数”,求出满足条件的一组实数对
)型函数”,求出满足条件的一组实数对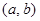 ;
;
(3)已知函数 是“
是“ 型函数”,对应的实数对
型函数”,对应的实数对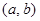 为
为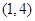 ,当
,当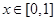 时,
时,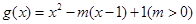 ,若当
,若当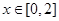 时,都有
时,都有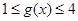 ,试求
,试求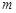 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知定义域为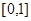 的函数
的函数 同时满足以下三个条件:
同时满足以下三个条件:
①对任意的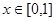 ,总有
,总有 ;
;
②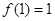 ;
;
③当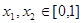 ,且
,且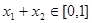 时,
时,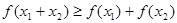 成立.
成立.
称这样的函数为“友谊函数”.
请解答下列各题:
(1)已知 为“友谊函数”,求
为“友谊函数”,求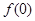 的值;
的值;
(2)函数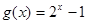 在区间
在区间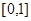 上是否为“友谊函数”?请给出理由;
上是否为“友谊函数”?请给出理由;
(3)已知 为“友谊函数”,假定存在
为“友谊函数”,假定存在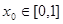 ,使得
,使得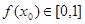 ,且
,且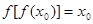 ,求证:
,求证: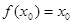 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2014·孝感模拟)已知定义在区间[0,2]上的两个函数f(x)和g(x),其中f(x)=-x2+2ax+1+a2,g(x)=x- +
+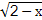 .
.
(1)求函数f(x)的最小值.
(2)对于?x1,x2∈[0,2],f(x1)>g(x2)恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com