
已知二次函数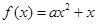
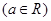
(1)当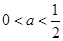 时,
时,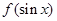
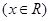 的最大值为
的最大值为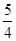 ,求
,求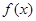 的最小值;
的最小值;
(2)对于任意的 ,总有
,总有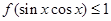 ,试求
,试求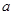 的取值范围.
的取值范围.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
甲、乙两个工厂,甲厂位于一直线河岸的岸边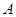 处,乙厂与甲厂在河的同侧,乙厂位于离河岸40千米的
处,乙厂与甲厂在河的同侧,乙厂位于离河岸40千米的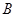 处,乙厂到河岸的垂足
处,乙厂到河岸的垂足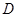 与
与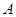 相距50千米,两厂要在此岸边
相距50千米,两厂要在此岸边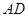 之间合建一个供水站
之间合建一个供水站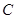 ,从供水站到甲厂和乙厂的水管费用分别为每千米3
,从供水站到甲厂和乙厂的水管费用分别为每千米3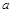 元和5
元和5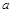 元,若
元,若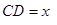 千米,设总的水管费用为
千米,设总的水管费用为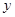 元,如图所示,
元,如图所示,
(1)写出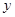 关于
关于 的函数表达式;
的函数表达式;
(2)问供水站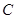 建在岸边何处才能使水管费用最省?
建在岸边何处才能使水管费用最省? 
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂生产一种产品的原材料费为每件40元,若用x表示该厂生产这种产品的总件数,则电力与机器保养等费用为每件0.05x元,又该厂职工工资固定支出12500元.
(1)把每件产品的成本费P(x)(元)表示成产品件数x的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量x不超过3000件,且产品能全部销售,根据市场调查:每件产品的销售价Q(x)与产品件数x有如下关系:Q(x)=170-0.05x,试问生产多少件产品时,总利润最高?(总利润=总销售额-总成本)
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
给出下列四个命题:
①函数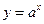 (
(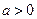 且
且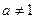 )与函数
)与函数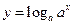 (
(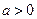 且
且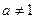 )的定义域相同;
)的定义域相同;
②函数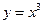 与
与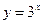 的值域相同;③函数
的值域相同;③函数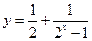 与
与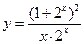 都是奇函数;④
都是奇函数;④
函数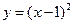 与
与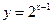 在区间
在区间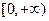 上都是增函数,其中正确命题的序号是_____________。(把你认为正确的命题序号都填上)
上都是增函数,其中正确命题的序号是_____________。(把你认为正确的命题序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com