
ij��������һ�ֲ�Ʒ��ԭ���Ϸ�Ϊÿ��40Ԫ������x��ʾ�ó��������ֲ�Ʒ���ܼ��������������������ȷ���Ϊÿ��0.05xԪ���ָó�ְ�����ʹ̶�֧��12500Ԫ��
(1)��ÿ����Ʒ�ijɱ���P(x)(Ԫ)��ʾ�ɲ�Ʒ����x�ĺ���������ÿ����Ʒ����ͳɱ��ѣ�
(2)����ó����������ֲ�Ʒ������x������3000�����Ҳ�Ʒ��ȫ�����ۣ������г����飺ÿ����Ʒ�����ۼ�Q(x)���Ʒ����x�����¹�ϵ��Q(x)��170��0.05x�������������ټ���Ʒʱ����������ߣ�(�����������۶�ܳɱ�)

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪���κ���f��x�����㣺�ٵ�x=1ʱ�м�ֵ����ͼ����y�ύ���������Ϊ��3�����ڸõ㴦��������ֱ��x=2y��4��ֱ��
��1����f��1����ֵ��
��2��������g��x��=f��lnx����x�ʣ�1��+�ޣ�������һ�㴦������б�ʺ����a2��a��2����ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪���κ���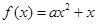
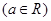
��1����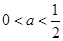 ʱ��
ʱ��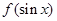
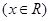 �����ֵΪ
�����ֵΪ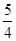 ����
����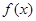 ����Сֵ��
����Сֵ��
��2����������� ������
������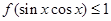 ������
������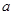 ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��һ����Ӣ�ĵ�����(��ʵ��)����ĸ�ֽ⣬����Ӣ�ĵ�a��b��c�� ��z��26����ĸ(���ִ�Сд)�����ζ�Ӧ1��2��3�� ��26��26����Ȼ���������±���:
| a | b | c | d | e | f | g | h | i | j | k | l | m |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| n | o | p | q | r | s | t | u | v | w | x | y | z |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
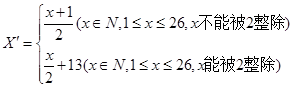
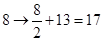 ����
����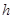 ���
��� ����
����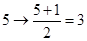 ����
����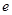 ���
���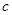 .
.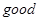 ��ɵ�������ʲô��
��ɵ�������ʲô�� ����ôԭ����������ʲô��
����ôԭ����������ʲô���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪����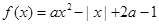 ��
�� Ϊʵ��������
Ϊʵ��������
��1����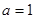 ������
������ �ĵ������䣻
�ĵ������䣻
��2���� ������
������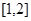 �ϵ���СֵΪ
�ϵ���СֵΪ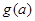 ����
����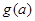 �ı���ʽ��
�ı���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪����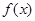 ����������
���������� ����
����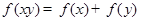 ���ҵ�
���ҵ�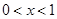 ʱ��
ʱ��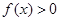 .
.
��1����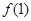 ��ֵ��
��ֵ��
��2���ж�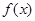 �ĵ�����
�ĵ�����
��3����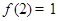 ���ⲻ��ʽ
���ⲻ��ʽ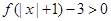 .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
���ں���f(x)������x0��R��f(x0)��x0���������x0Ϊf(x)�IJ����㣮��֪f(x)��ax2��(b��1)x��b��1(a��0)��
(1)��a��1��b����2ʱ������f(x)�IJ����㣻
(2)��������ʵ��b������f(x)������������IJ����㣬��a��ȡֵ��Χ��
(3)��(2)�������£���y��f(x)ͼ����A��B����ĺ������Ǻ���f(x)�IJ����㣬��A��B�������ֱ��y��kx��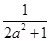 �Գƣ���b����Сֵ��
�Գƣ���b����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
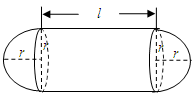
ij����վ������ͼ��ʾ����Ƥ���ޣ����ƺ�ȣ����ȵ�λ���ף������д����м�ΪԲ���Σ��������˾�Ϊ�����Σ�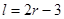 ��
��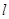 ΪԲ���ĸߣ�
ΪԲ���ĸߣ�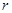 Ϊ��İ뾶��
Ϊ��İ뾶��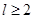 ��.����ô��Ľ�����ý����������й�.��֪Բ���β���ÿƽ���������Ϊ
��.����ô��Ľ�����ý����������й�.��֪Բ���β���ÿƽ���������Ϊ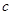 ǧԪ�������β���ÿƽ���������Ϊ3ǧԪ.��ô��Ľ������Ϊ
ǧԪ�������β���ÿƽ���������Ϊ3ǧԪ.��ô��Ľ������Ϊ ǧԪ.
ǧԪ.
��1��� ����
����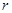 �ĺ�������ʽ������ú����Ķ�����
�ĺ�������ʽ������ú����Ķ�����
��2����ô��Ľ��������Сʱ��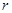 ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�躯��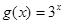 ��
��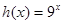 .
.
��1���ⷽ�̣�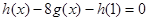 ��
��
��2����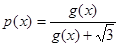 ����֤��
����֤��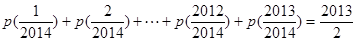 ��
��
��3����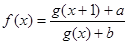 ��ʵ����
��ʵ���� �ϵ��溯������
�ϵ��溯������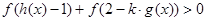 ������ʵ��
������ʵ�� ���������ʵ��
���������ʵ�� ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com