
已知二次函数f(x)满足:①当x=1时有极值;②图象与y轴交点的纵坐标为﹣3,且在该点处的切线与直线x=2y﹣4垂直.
(1)求f(1)的值;
(2)若函数g(x)=f(lnx),x∈(1,+∞)上任意一点处的切线斜率恒大于a2﹣a﹣2,求实数a的取值范围.
(I)-4;(II)0≤a≤1.
解析试题分析:(1)由已知可利用待定系数法,首先设二次函数f(x)的解析式为:f(x)=ax2+bx+c,,结合已知的两个条件及导数的几何意义,求出f(x)的表达式,从而可求f(1)的值;
(2)首先求出g(x)的表达式,利用导数求出切线斜率,结合一元二次不等式的解法即可得到结论.
试题解析:(1)设二次函数f(x)=ax2+bx+c,
∵x=1时有极值,∴对称轴为1,即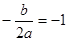 ,
,
由②知f(0)=c=-3,在(0,-3)处的切线斜率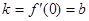 ,
,
又在该点处的切线与直线x=2y-4垂直,故b=-2,
解得a=1,则f(x)=x2-2x-3,
则f(1)=-4;
(2)若函数g(x)=f(lnx)=(lnx)2-2lnx-3,
令t=lnx,
则∵x∈(1,+∞),∴t∈(0,+∞),
∴f(t)=t2-2t-3,f′(t)=2t-2>-2,
若函数g(x)=f(lnx),x∈(1,+∞)上任意一点处的切线斜率恒大于a2-a-2,
则f′(t)>a2-a-2恒成立,即a2-a-2≤-2,
即a2-a≤0,解得0≤a≤1.
考点:1.二次函数的图象和性质;2.导数的几何意义.


科目:高中数学 来源: 题型:解答题
制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目.根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损分别为30%和10%.投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元.问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂生产一种产品的原材料费为每件40元,若用x表示该厂生产这种产品的总件数,则电力与机器保养等费用为每件0.05x元,又该厂职工工资固定支出12500元.
(1)把每件产品的成本费P(x)(元)表示成产品件数x的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量x不超过3000件,且产品能全部销售,根据市场调查:每件产品的销售价Q(x)与产品件数x有如下关系:Q(x)=170-0.05x,试问生产多少件产品时,总利润最高?(总利润=总销售额-总成本)
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
给出下列四个命题:
①函数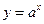 (
(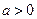 且
且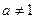 )与函数
)与函数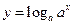 (
(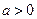 且
且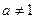 )的定义域相同;
)的定义域相同;
②函数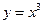 与
与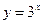 的值域相同;③函数
的值域相同;③函数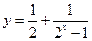 与
与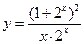 都是奇函数;④
都是奇函数;④
函数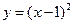 与
与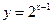 在区间
在区间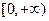 上都是增函数,其中正确命题的序号是_____________。(把你认为正确的命题序号都填上)
上都是增函数,其中正确命题的序号是_____________。(把你认为正确的命题序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com