
有一种密英文的明文(真实文)按字母分解,其中英文的a,b,c, ,z的26个字母(不分大小写),依次对应1,2,3, ,26这26个自然数,见如下表格:
| a | b | c | d | e | f | g | h | i | j | k | l | m |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| n | o | p | q | r | s | t | u | v | w | x | y | z |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
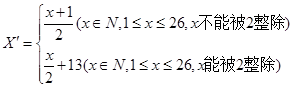
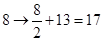 ,即
,即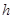 变成
变成 ;如
;如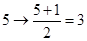 ,即
,即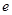 变成
变成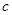 .
.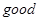 译成的密文是什么?
译成的密文是什么? ,那么原来的明文是什么?
,那么原来的明文是什么? (1)明文good的密文为dhho;(2)密文shxc的明文为love.
解析试题分析:(1)由题意先找出“good”中各个字母对应的数,判断出奇偶数,然后依据不同的解析式进行翻译成数,然后根据数与字母的对应关系,将相应的数变成字母,这样就得到了“good”的密文;(2)先逆变换公式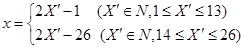 ,进而找出“shxc”中各字母对应的数,由对应的数的范围选择不同的解析式进行翻译成数,再由数与字母的对应关系,将数变成字母,这样就得到了“shxc”的明文.
,进而找出“shxc”中各字母对应的数,由对应的数的范围选择不同的解析式进行翻译成数,再由数与字母的对应关系,将数变成字母,这样就得到了“shxc”的明文.
(1)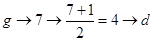 ;
;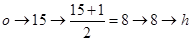 ;
;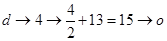
所以明文good的密文为dhho 5分
(2)逆变换公式为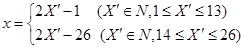
则有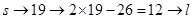 ;
;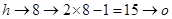
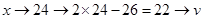 ;
;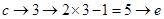
故密文shxc的明文为love 10分
考点:1.函数的解析式;2.分段函数;3.函数的实际应用.


科目:高中数学 来源: 题型:解答题
已知函数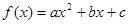 (a≠0)满足
(a≠0)满足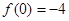 ,
,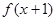 为偶函数,且x=-2是函数
为偶函数,且x=-2是函数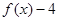 的一个零点.又
的一个零点.又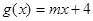 (
( >0).
>0).
(1)求函数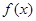 的解析式;
的解析式;
(2)若关于x 的方程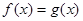 在
在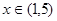 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
(3)令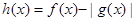 ,求
,求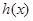 的单调区间.
的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂生产一种产品的原材料费为每件40元,若用x表示该厂生产这种产品的总件数,则电力与机器保养等费用为每件0.05x元,又该厂职工工资固定支出12500元.
(1)把每件产品的成本费P(x)(元)表示成产品件数x的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量x不超过3000件,且产品能全部销售,根据市场调查:每件产品的销售价Q(x)与产品件数x有如下关系:Q(x)=170-0.05x,试问生产多少件产品时,总利润最高?(总利润=总销售额-总成本)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)(2011•湖北)提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(Ⅰ)当0≤x≤200时,求函数v(x)的表达式;
(Ⅱ)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=x•v(x)可以达到最大,并求出最大值.(精确到1辆/小时).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com