
设函数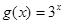 ,
,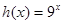 .
.
(1)解方程: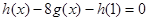 ;
;
(2)令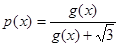 ,求证:
,求证: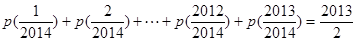 ;
;
(3)若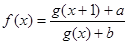 是实数集
是实数集 上的奇函数,且
上的奇函数,且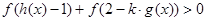 对任意实数
对任意实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1)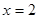 ;(2)参考解析;(3)
;(2)参考解析;(3)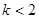
解析试题分析:(1)由于函数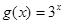 ,
,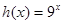 ,所以解方程
,所以解方程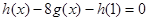 .通过换元即可转化为解二次方程.即可求得结论.
.通过换元即可转化为解二次方程.即可求得结论.
(2)由于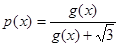 即得到
即得到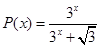 .所以
.所以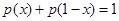 .所以两个一组的和为1,还剩中间一个
.所以两个一组的和为1,还剩中间一个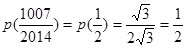 .即可求得结论.
.即可求得结论.
(3)由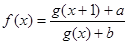 是实数集
是实数集 上的奇函数,可求得
上的奇函数,可求得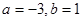 .又由于
.又由于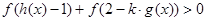 对任意实数
对任意实数 恒成立.该式的理解较困难,所以研究函数
恒成立.该式的理解较困难,所以研究函数 的单调性可得.函数
的单调性可得.函数 在实数集上是递增.集合奇函数,由函数值大小即可得到变量的大小,再利用基本不等式,从而得到结论.
在实数集上是递增.集合奇函数,由函数值大小即可得到变量的大小,再利用基本不等式,从而得到结论.
试题解析:(1)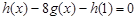 即:
即: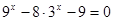 ,解得
,解得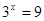 ,
,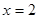
(2)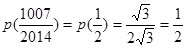 .
.
因为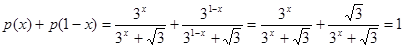 ,
,
所以,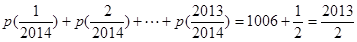 ,
,
(3)因为 是实数集上的奇函数,所以
是实数集上的奇函数,所以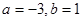 .
.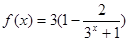 ,
, 在实数集上单调递增.
在实数集上单调递增.
由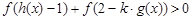 得
得 ,又因为
,又因为 是实数集上的奇函数,所以,
是实数集上的奇函数,所以,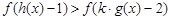 ,
,
又因为 在实数集上单调递增,所以
在实数集上单调递增,所以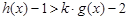
即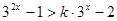 对任意的
对任意的 都成立,
都成立,
即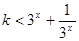 对任意的
对任意的 都成立,
都成立,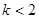 .
.
考点:1.解方程的思想.2.函数的单调性.3.归纳推理的思想.4.基本不等式.


科目:高中数学 来源: 题型:解答题
某工厂生产一种产品的原材料费为每件40元,若用x表示该厂生产这种产品的总件数,则电力与机器保养等费用为每件0.05x元,又该厂职工工资固定支出12500元.
(1)把每件产品的成本费P(x)(元)表示成产品件数x的函数,并求每件产品的最低成本费;
(2)如果该厂生产的这种产品的数量x不超过3000件,且产品能全部销售,根据市场调查:每件产品的销售价Q(x)与产品件数x有如下关系:Q(x)=170-0.05x,试问生产多少件产品时,总利润最高?(总利润=总销售额-总成本)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,长方形物体E在雨中沿面P(面积为S)的垂直方向作匀速移动,速度为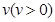 ,雨速沿E移动方向的分速度为
,雨速沿E移动方向的分速度为 。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与
。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与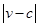 ×S成正比,比例系数为
×S成正比,比例系数为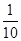 ;(2)其它面的淋雨量之和,其值为
;(2)其它面的淋雨量之和,其值为 ,记
,记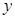 为E移动过程中的总淋雨量,当移动距离d=100,面积S=
为E移动过程中的总淋雨量,当移动距离d=100,面积S=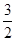 时。
时。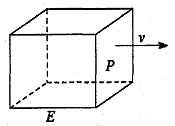
(1)写出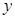 的表达式
的表达式
(2)设0<v≤10,0<c≤5,试根据c的不同取值范围,确定移动速度 ,使总淋雨量
,使总淋雨量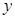 最少。
最少。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某公司以每吨10万元的价格销售某种产品,每年可售出该产品1000吨,若将该产品每吨的价格上涨x%,则每年的销售数量将减少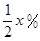 ,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为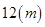 ,高
,高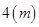 ,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大
,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大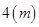 (高不变);二是高度增加
(高不变);二是高度增加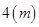 (底面直径不变)。
(底面直径不变)。
(1)分别计算按这两种方案所建的仓库的体积;
(2)分别计算按这两种方案所建的仓库的表面积(地面无需用材料);
(3)哪个方案更经济些?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对于函数 ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足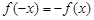 ,则称
,则称 为“局部奇函数”.
为“局部奇函数”.
(1)已知函数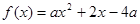
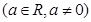 ,试判断
,试判断 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)若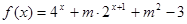 为定义域
为定义域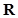 上的“局部奇函数”,求实数m的取值范围.
上的“局部奇函数”,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com