
某公司以每吨10万元的价格销售某种产品,每年可售出该产品1000吨,若将该产品每吨的价格上涨x%,则每年的销售数量将减少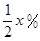 ,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:解答题
已知函数f(x)的图象与函数h(x)=x+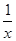 +2的图象关于点A(0,1)对称.
+2的图象关于点A(0,1)对称.
(1)求f(x)的解析式;
(2)若g(x)=f(x)·x+ax,且g(x)在区间[0,2]上为减函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数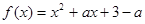 ,
,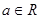 .
.
(1)求 的取值范围,使
的取值范围,使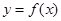 在闭区间
在闭区间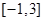 上是单调函数;
上是单调函数;
(2)当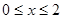 时,函数
时,函数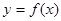 的最大值是关于
的最大值是关于 的函数
的函数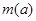 .求
.求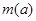 ;
;
(3)求实数 的取值范围,使得对任意的
的取值范围,使得对任意的
 ,恒有
,恒有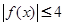 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某通讯公司需要在三角形地带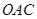 区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域
区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域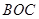 内,乙中转站建在区域
内,乙中转站建在区域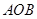 内.分界线
内.分界线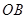 固定,且
固定,且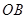 =
=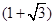 百米,边界线
百米,边界线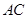 始终过点
始终过点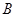 ,边界线
,边界线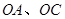 满足
满足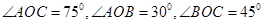 .
.
设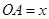 (
(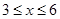 )百米,
)百米,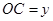 百米.
百米.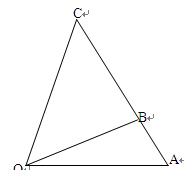
(1)试将 表示成
表示成 的函数,并求出函数
的函数,并求出函数 的解析式;
的解析式;
(2)当 取何值时?整个中转站的占地面积
取何值时?整个中转站的占地面积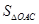 最小,并求出其面积的最小值.
最小,并求出其面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对于函数 ,若在定义域存在实数
,若在定义域存在实数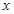 ,满足
,满足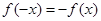 ,则称
,则称 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数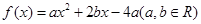 ,试判断
,试判断 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)设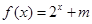 是定义在
是定义在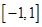 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数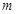 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知两条直线l1:y=m和l2:y=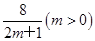 ,l1与函数y=|log2x|的图象从左至右相交于点A、B,l2与函数y=|log2x|的图象从左至右相交于点C、D.记线段AC和BD在x轴上的投影长度分别为a、b.当m变化时,求
,l1与函数y=|log2x|的图象从左至右相交于点A、B,l2与函数y=|log2x|的图象从左至右相交于点C、D.记线段AC和BD在x轴上的投影长度分别为a、b.当m变化时,求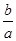 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com