
某通讯公司需要在三角形地带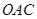 区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域
区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域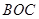 内,乙中转站建在区域
内,乙中转站建在区域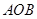 内.分界线
内.分界线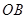 固定,且
固定,且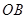 =
=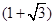 百米,边界线
百米,边界线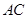 始终过点
始终过点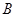 ,边界线
,边界线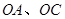 满足
满足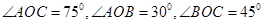 .
.
设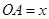 (
(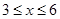 )百米,
)百米,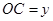 百米.
百米.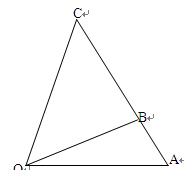
(1)试将 表示成
表示成 的函数,并求出函数
的函数,并求出函数 的解析式;
的解析式;
(2)当 取何值时?整个中转站的占地面积
取何值时?整个中转站的占地面积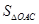 最小,并求出其面积的最小值.
最小,并求出其面积的最小值.
(1)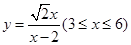 ;(2):当
;(2):当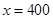 米时,整个中转站的占地面积
米时,整个中转站的占地面积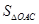 最小,最小面积是
最小,最小面积是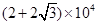 平方米.
平方米.
解析试题分析:(1)要求函数关系式,实际上是建立起 之间的等量关系,分析图形及已知条件,我们可借助于三角形有面积,
之间的等量关系,分析图形及已知条件,我们可借助于三角形有面积,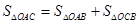 ,从这个等式中,解出
,从这个等式中,解出 ,即得要求的函数式;(2)有了(1)中的关系式,
,即得要求的函数式;(2)有了(1)中的关系式, 就可表示为一个字母
就可表示为一个字母 的式子
的式子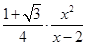 ,它是一个分式函数,由于分母是一次,而分子是二次的,故可这样变形
,它是一个分式函数,由于分母是一次,而分子是二次的,故可这样变形 ,正好这个表达式可以用基本不等式来求得最小值.
,正好这个表达式可以用基本不等式来求得最小值.
试题解析:(1)结合图形可知,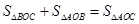 .
.
于是,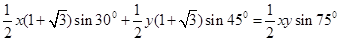 ,
,
解得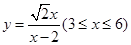 .
.
(2)由(1)知,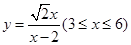 ,
,
因此,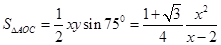

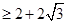 (当且仅当
(当且仅当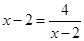 ,即
,即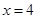 时,等号成立).
时,等号成立).
答:当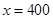 米时,整个中转站的占地面积
米时,整个中转站的占地面积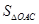 最小,最小面积是
最小,最小面积是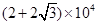 平方米.12分
平方米.12分
考点:求函数解析式,三角形的面积公式,分式函数的最值与基本不等式.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
已知二次函数f(x)=ax2+bx+c (a≠0)且满足f(-1)=0,对任意实数x,恒有f(x)-x≥0,并且当x∈(0,2)时,f(x)≤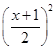 .
.
(1)求f(1)的值;
(2)证明:a>0,c>0;
(3)当x∈[-1,1]时,函数g(x)=f(x)-mx (x∈R)是单调函数,求证:m≤0或m≥1.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市2013年发放汽车牌照12万张,其中燃油型汽车牌照10万张,电动型汽车2万张.为了节能减排和控制总量,从2013年开始,每年电动型汽车牌照按50%增长,而燃油型汽车牌照每一年比上一年减少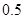 万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.
万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.
(1)记2013年为第一年,每年发放的燃油型汽车牌照数构成数列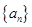 ,每年发放的电动型汽车牌照数为构成数列
,每年发放的电动型汽车牌照数为构成数列 ,完成下列表格,并写出这两个数列的通项公式;
,完成下列表格,并写出这两个数列的通项公式;
(2)从2013年算起,求二十年发放的汽车牌照总量.
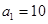 | 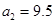 | 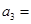 | 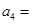 | |
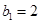 |  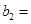 3 3 | 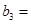 | 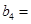 | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某公司以每吨10万元的价格销售某种产品,每年可售出该产品1000吨,若将该产品每吨的价格上涨x%,则每年的销售数量将减少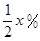 ,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校要建一个面积为450平方米的矩形球场,要求球场的一面利用旧墙,其他各面用钢筋网围成,且在矩形一边的钢筋网的正中间要留一个3米的进出口(如图).设矩形的长为 米,钢筋网的总长度为
米,钢筋网的总长度为 米.
米.
(1)列出 与
与 的函数关系式,并写出其定义域;
的函数关系式,并写出其定义域;
(2)问矩形的长与宽各为多少米时,所用的钢筋网的总长度最小?
(3)若由于地形限制,该球场的长和宽都不能超过25米,问矩形的长与宽各为多少米时,所用的钢筋网的总长度最小?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=x2+mx+n的图象过点(1,3),且f(-1+x)=f(-1-x)对任意实数都成立,函数y=g(x)与y=f(x)的图象关于原点对称.
(1)求f(x)与g(x)的解析式;
(2)若F(x)=g(x)-λf(x)在(-1,1]上是增函数,求实数λ的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com