
某校要建一个面积为450平方米的矩形球场,要求球场的一面利用旧墙,其他各面用钢筋网围成,且在矩形一边的钢筋网的正中间要留一个3米的进出口(如图).设矩形的长为 米,钢筋网的总长度为
米,钢筋网的总长度为 米.
米.
(1)列出 与
与 的函数关系式,并写出其定义域;
的函数关系式,并写出其定义域;
(2)问矩形的长与宽各为多少米时,所用的钢筋网的总长度最小?
(3)若由于地形限制,该球场的长和宽都不能超过25米,问矩形的长与宽各为多少米时,所用的钢筋网的总长度最小?
(1)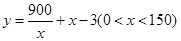
(2)长为30米,宽为15米,所用的钢筋网的总长度最小.
(3)长为25米,宽为18米时,所用的钢筋网的总长度最小
解析试题分析:(1)根据矩形的面积求出解析式,注意函数的定义域
(2)利用基本不等式求解,注意等号成立的条件
(3)利用函数的单调性求解(导数或单调性定义)
试题解析:(1)矩形的宽为: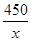 米
米 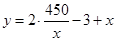
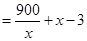
定义域为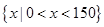
注:定义域为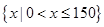 不扣分
不扣分
(2)
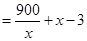
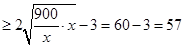
当且仅当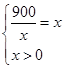 即
即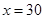 时取等号,此时宽为:
时取等号,此时宽为: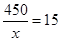 米
米
所以,长为30米,宽为15米,所用的钢筋网的总长度最小.
(3)法一:
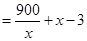
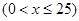 ,
,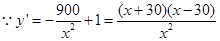
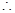 当
当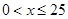 时,
时,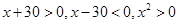
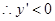
 在
在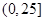 上是单调递减函数
上是单调递减函数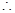 当
当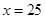 时,
时,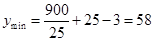 ,此时,长为25米,宽为
,此时,长为25米,宽为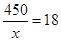 米
米
所以,长为25米,宽为18米时,所用的钢筋网的总长度最小.
法二:设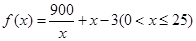 ,
,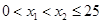 ,
,
则 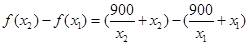
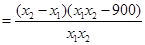
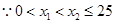 ,
,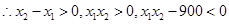
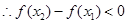 ,
, 
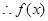 在
在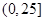 上是单调递减函数
上是单调递减函数 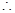 当
当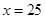 时,
时,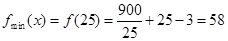
此时,长为25米,宽为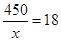 米
米
所以,长为25米,宽为18米时,所用的钢筋网的总长度最小.
考点:基本不等式的应用,函数的单调性,最值


科目:高中数学 来源: 题型:解答题
已知函数f(x)=3x-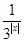 .
.
(1)若f(x)=2,求x的值;
(2)判断x>0时,f(x)的单调性;
(3)若3tf(2t)+mf(t)≥0对于t∈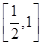 恒成立,求m的取值范围.
恒成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数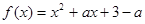 ,
,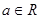 .
.
(1)求 的取值范围,使
的取值范围,使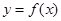 在闭区间
在闭区间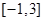 上是单调函数;
上是单调函数;
(2)当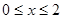 时,函数
时,函数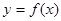 的最大值是关于
的最大值是关于 的函数
的函数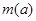 .求
.求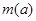 ;
;
(3)求实数 的取值范围,使得对任意的
的取值范围,使得对任意的
 ,恒有
,恒有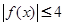 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某通讯公司需要在三角形地带 区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域
区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域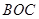 内,乙中转站建在区域
内,乙中转站建在区域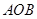 内.分界线
内.分界线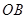 固定,且
固定,且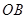 =
=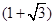 百米,边界线
百米,边界线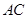 始终过点
始终过点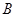 ,边界线
,边界线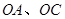 满足
满足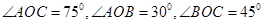 .
.
设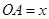 (
(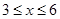 )百米,
)百米,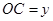 百米.
百米.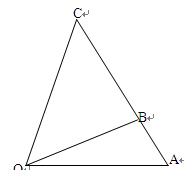
(1)试将 表示成
表示成 的函数,并求出函数
的函数,并求出函数 的解析式;
的解析式;
(2)当 取何值时?整个中转站的占地面积
取何值时?整个中转站的占地面积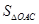 最小,并求出其面积的最小值.
最小,并求出其面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对于函数 ,若在定义域存在实数
,若在定义域存在实数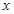 ,满足
,满足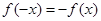 ,则称
,则称 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数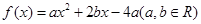 ,试判断
,试判断 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)设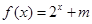 是定义在
是定义在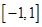 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数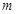 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知 的图象关于坐标原点对称。
的图象关于坐标原点对称。
(1)求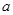 的值,并求出函数
的值,并求出函数 的零点;
的零点;
(2)若函数 在[0,1]内存在零点,求实数b的取值范围;
在[0,1]内存在零点,求实数b的取值范围;
(3)设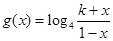 ,已知
,已知 的反函数
的反函数 =
= ,若不等式
,若不等式 在
在 上恒成立,求满足条件的最小整数k的值。
上恒成立,求满足条件的最小整数k的值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
经市场调查,某种商品在过去50天的销量和价格均为销售时间t(天)的函数,且销售量近似地满足f(t)=-2t+200(1≤t≤50,t∈N),前30天价格为g(t)= t+30(1≤t≤30,t∈N),后20天价格为g(t)=45(31≤t≤50,t∈N).
t+30(1≤t≤30,t∈N),后20天价格为g(t)=45(31≤t≤50,t∈N).
(1)写出该种商品的日销售额S与时间t的函数关系式;
(2)求日销售额S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=x2-4,设曲线y=f(x)在点(xn,f(xn))
处的切线与x轴的交点为(xn+1,0)(n∈N+),其中x1为正实数.
(1)用xn表示xn+1;
(2)求证:对一切正整数n,xn+1≤xn的充要条件是x1≥2;
(3)若x1=4,记an=lg  ,证明数列{an}成等比数列,并求数列{xn}的通项公式.
,证明数列{an}成等比数列,并求数列{xn}的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com