练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)＝3x－.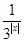
    (1)若f(x)＝2，求x的值；
    (2)判断x>0时，f(x)的单调性；
    (3)若3tf(2t)＋mf(t)≥0对于t∈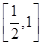恒成立，求m的取值范围．

    （1）log3(1＋)
    （2）f(x)＝3x－在(0，＋∞)上单调递增
    （3）[－4，＋∞)

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    某单位有员工1000名，平均每人每年创造利润10万元。为了增加企业竞争力，决定优化产业结构，调整出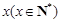名员工从事第三产业，调整后他们平均每人每年创造利为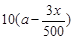万元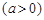，剩下的员工平均每人每年创造的利润可以提高.
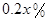    （1）若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润，则最多调整出多少名员工从事第三产业？
    （2）在（1）的条件下，若调整出的员工创造的年总利润始终不高于剩余员工创造的年总利润，则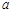的取值范围是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数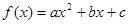（a≠0）满足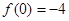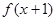，为偶函数，且x＝－2是函数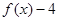的一个零点．又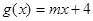（＞0）．
    （1）求函数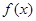的解析式；
    （2）若关于x 的方程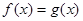在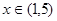上有解，求实数的取值范围；
    （3）令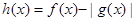，求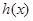的单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数f(x)＝xm－且f(4)＝.
    (1)求m的值；
    (2)判定f(x)的奇偶性；
    (3)判断f(x)在(0，＋∞)上的单调性，并给予证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （12分）（2011•湖北）提高过江大桥的车辆通行能力可改善整个城市的交通状况，在一般情况下，大桥上的车流速度v（单位：千米/小时）是车流密度x（单位：辆/千米）的函数，当桥上的车流密度达到200辆/千米时，造成堵塞，此时车流速度为0；当车流密度不超过20辆/千米时，车流速度为60千米/小时，研究表明：当20≤x≤200时，车流速度v是车流密度x的一次函数．
    （Ⅰ）当0≤x≤200时，求函数v（x）的表达式；
    （Ⅱ）当车流密度x为多大时，车流量（单位时间内通过桥上某观测点的车辆数，单位：辆/小时）f（x）=x•v（x）可以达到最大，并求出最大值．（精确到1辆/小时）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知中心在原点，焦点在轴上的椭圆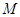的离心率为，椭圆上异于长轴顶点的任意点与左右两焦点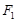、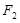构成的三角形中面积的最大值为.
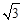    （1）求椭圆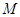的标准方程；
    （2）已知点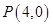，连接与椭圆的另一交点记为，若与椭圆相切时、不重合，连接与椭圆的另一交点记为，求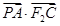的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数定义在上，对任意的，，且.
    （1）求，并证明：；
    （2）若单调，且.设向量，对任意，恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知二次函数f(x)＝ax2＋bx＋c (a≠0)且满足f(－1)＝0，对任意实数x，恒有f(x)－x≥0，并且当x∈(0,2)时，f(x)≤.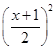
    (1)求f(1)的值；
    (2)证明：a>0，c>0；
    (3)当x∈[－1,1]时，函数g(x)＝f(x)－mx (x∈R)是单调函数，求证：m≤0或m≥1.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某校要建一个面积为450平方米的矩形球场，要求球场的一面利用旧墙，其他各面用钢筋网围成，且在矩形一边的钢筋网的正中间要留一个3米的进出口（如图）．设矩形的长为米，钢筋网的总长度为米．

    （1）列出与的函数关系式，并写出其定义域；
    （2）问矩形的长与宽各为多少米时，所用的钢筋网的总长度最小？
    （3）若由于地形限制，该球场的长和宽都不能超过25米，问矩形的长与宽各为多少米时，所用的钢筋网的总长度最小？

    查看答案和解析>>

    同步练习册答案