
某单位有员工1000名,平均每人每年创造利润10万元。为了增加企业竞争力,决定优化产业结构,调整出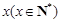 名员工从事第三产业,调整后他们平均每人每年创造利为
名员工从事第三产业,调整后他们平均每人每年创造利为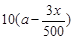 万元
万元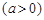 ,剩下的员工平均每人每年创造的利润可以提高
,剩下的员工平均每人每年创造的利润可以提高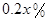 .
.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(2)在(1)的条件下,若调整出的员工创造的年总利润始终不高于剩余员工创造的年总利润,则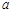 的取值范围是多少?
的取值范围是多少?
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:解答题
某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形休闲区A1B1C1D1和环公园人行道(阴影部分)组成.已知休闲区A1B1C1D1的面积为4000m2,人行道的宽分别为4m和10m(如图所示).
(1)若设休闲区的长和宽的比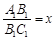 ,求公园ABCD所占面积S关于x的函数解析式;
,求公园ABCD所占面积S关于x的函数解析式;
(2)要使公园所占面积最小,休闲区A1B1C1D1的长和宽应如何设计?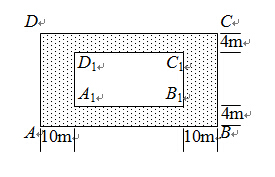
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
销售甲、乙两种商品所得利润分别为P(单位:万元)和Q(单位:万元),它们与投入资金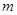 (单位:万元)的关系有经验公式
(单位:万元)的关系有经验公式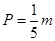 ,
, 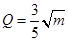 . 今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资
. 今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资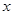 (单位:万元)
(单位:万元)
(1)试建立总利润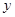 (单位:万元)关于
(单位:万元)关于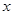 的函数关系式,并指明函数定义域;
的函数关系式,并指明函数定义域;
(2)如何投资经营甲、乙两种商品,才能使得总利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,制图工程师要用两个同中心的边长均为4的正方形合成一个八角形图形.由对称性,图中8个三角形都是全等的三角形,设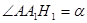 .
.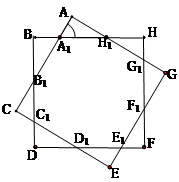
(1)试用 表示
表示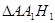 的面积;
的面积;
(2)求八角形所覆盖面积的最大值,并指出此时 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=3x-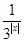 .
.
(1)若f(x)=2,求x的值;
(2)判断x>0时,f(x)的单调性;
(3)若3tf(2t)+mf(t)≥0对于t∈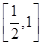 恒成立,求m的取值范围.
恒成立,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com