
设二次函数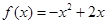 .
.
(1)求函数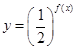 的最小值;
的最小值;
(2)问是否存在这样的正数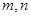 ,当
,当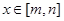 时,
时,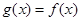 ,且
,且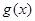 的值域为
的值域为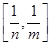 ?若存在,求出所有的
?若存在,求出所有的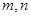 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
(1)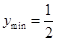 ;(2)
;(2)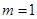 ,
,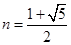 .
.
解析试题分析:(1)这里遇到的是复合函数的最值问题,它是由简单的二次函数与指数函数复合而成的,遵循由内到外的解题顺序,很容易求出最小值;(2)这里是含参数的问题,常规方法是对参数分类讨论,如何分类,即分类的标准是什么?这是重点和难点,看解析往往是知其然,不知其所以然,这里的分类标准是将动区间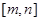 与二次函数
与二次函数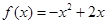 的定对称轴
的定对称轴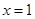 进行比较,自然就会分出它们有三种相对位置关系,即对称轴
进行比较,自然就会分出它们有三种相对位置关系,即对称轴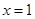 分别在区间
分别在区间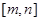 的左、中、右,故讨论分三种情形,当然讨论必须遵守不重不漏的原则,因此我们还必须关注细节,如区间的端点等,学会讨论重要,学会回避讨论更重要,它对化繁为简的能力要求非常高,这里的解法一是分类讨论的,而解法二就回避了讨论,解得很简洁,用心体会一下.
的左、中、右,故讨论分三种情形,当然讨论必须遵守不重不漏的原则,因此我们还必须关注细节,如区间的端点等,学会讨论重要,学会回避讨论更重要,它对化繁为简的能力要求非常高,这里的解法一是分类讨论的,而解法二就回避了讨论,解得很简洁,用心体会一下.
试题解析:(1)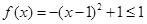 ,令
,令
则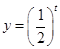 为
为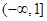 上减函数,因此,则当
上减函数,因此,则当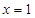 时,
时,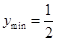 4分
4分
(2)法一:
①当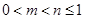 时,
时,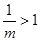
而当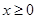 时,
时,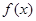 的最大值为
的最大值为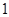 ,故此时不可能使
,故此时不可能使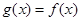 ,且
,且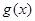 的值域为
的值域为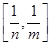 .7分
.7分
②当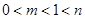 时,
时,
则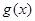 最大值为
最大值为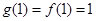 ,即
,即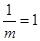 ,
,
得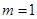 与
与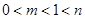 矛盾,故此时不可能. 10分
矛盾,故此时不可能. 10分
③当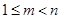 时,
时,
∵ ,
,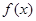 为减函数,则
为减函数,则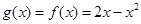
于是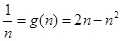 ,即
,即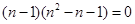 ,
,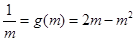
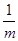 ,即
,即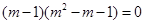
∵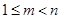 ,∴
,∴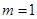 ,
,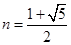 13分
13分
综上所述,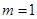 ,
,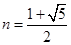 . 14分
. 14分
法二: ,
,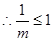 ,即
,即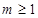 ,即
,即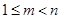 ,
,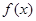 为
为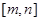 减函数,
减函数,
于是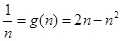 ,即
,即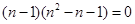 ,
,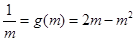
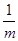 ,即
,即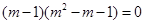
∵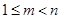 ,∴
,∴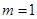 ,
,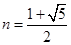 14分
14分
考点:1.函数性质的研究;2.含参数问题的讨论;3.函数、方程与不等式的综合.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目.根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损分别为30%和10%.投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元.问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位有员工1000名,平均每人每年创造利润10万元。为了增加企业竞争力,决定优化产业结构,调整出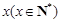 名员工从事第三产业,调整后他们平均每人每年创造利为
名员工从事第三产业,调整后他们平均每人每年创造利为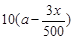 万元
万元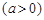 ,剩下的员工平均每人每年创造的利润可以提高
,剩下的员工平均每人每年创造的利润可以提高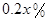 .
.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(2)在(1)的条件下,若调整出的员工创造的年总利润始终不高于剩余员工创造的年总利润,则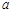 的取值范围是多少?
的取值范围是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com