
已知命题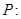 函数
函数 在区间
在区间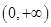 上是单调递增函数;命题
上是单调递增函数;命题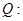 不等式
不等式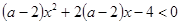 对任意实数
对任意实数 恒成立.若
恒成立.若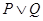 是真命题,且
是真命题,且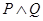 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
为了研究玉米品种对产量的影响,某农科院对一块试验田种植的一批玉米共10000株的生长情况进行研究,现采用分层抽样方法抽取50株为样本,统计结果如下:
| | 高茎 | 矮茎 | 合计 |
| 圆粒 | 11 | 19 | 30 |
| 皱粒 | 13 | 7 | 20 |
| 合计 | 24 | 26 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
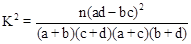 ,其中n=a+b+c+d为样本容量.
,其中n=a+b+c+d为样本容量.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
销售甲、乙两种商品所得利润分别为P(单位:万元)和Q(单位:万元),它们与投入资金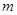 (单位:万元)的关系有经验公式
(单位:万元)的关系有经验公式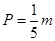 ,
, 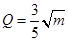 . 今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资
. 今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资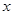 (单位:万元)
(单位:万元)
(1)试建立总利润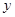 (单位:万元)关于
(单位:万元)关于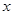 的函数关系式,并指明函数定义域;
的函数关系式,并指明函数定义域;
(2)如何投资经营甲、乙两种商品,才能使得总利润最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com