
已知 是定义在
是定义在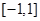 上的奇函数,且
上的奇函数,且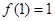 ,若
,若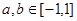 ,
,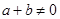 有
有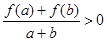 恒成立.
恒成立.
(1)判断 在
在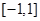 上是增函数还是减函数,并证明你的结论;
上是增函数还是减函数,并证明你的结论;
(2)若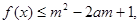 对所有
对所有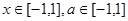 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
经过长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量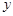 (千辆/时)与汽车的平均速度
(千辆/时)与汽车的平均速度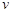 (千米/时)之间的函数关系为
(千米/时)之间的函数关系为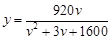 (
(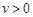 ).
).
(1)在该时段内,当汽车的平均速度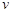 为多少时,车流量最大?最大车流量为多少?
为多少时,车流量最大?最大车流量为多少?
(2)若要求在该时段内车流量超过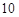 千辆/时,则汽车的平均速度应在什么范围内?
千辆/时,则汽车的平均速度应在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数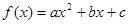 (a≠0)满足
(a≠0)满足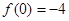 ,
,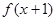 为偶函数,且x=-2是函数
为偶函数,且x=-2是函数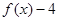 的一个零点.又
的一个零点.又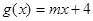 (
( >0).
>0).
(1)求函数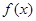 的解析式;
的解析式;
(2)若关于x 的方程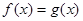 在
在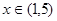 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
(3)令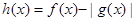 ,求
,求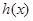 的单调区间.
的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
轮滑是穿着带滚轮的特制鞋在坚硬的场地上滑行的运动.如图,助跑道ABC是一段抛物线,某轮滑运动员通过助跑道获取速度后飞离跑道然后落到离地面高为1 m的平台上E处,飞行的轨迹是一段抛物线CDE(抛物线CDE与抛物线ABC在同一平面内),D为这段抛物线的最高点.现在运动员的滑行轮迹所在平面上建立如图所示的直角坐标系,x轴在地面上,助跑道一端点A(0,4),另一端点C(3,1),点B(2,0),单位:m.
(1)求助跑道所在的抛物线方程;
(2)若助跑道所在抛物线与飞行轨迹所在抛物线在点C处有相同的切线,为使运动员安全和空中姿态优美,要求运动员的飞行距离在4 m到6 m之间(包括4 m和6 m),试求运动员飞行过程中距离平台最大高度的取值范围.
(注:飞行距离指点C与点E的水平距离,即这两点横坐标差的绝对值)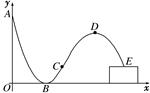
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知中心在原点,焦点在 轴上的椭圆
轴上的椭圆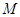 的离心率为
的离心率为 ,椭圆上异于长轴顶点的任意点
,椭圆上异于长轴顶点的任意点 与左右两焦点
与左右两焦点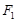 、
、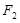 构成的三角形中面积的最大值为
构成的三角形中面积的最大值为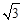 .
.
(1)求椭圆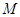 的标准方程;
的标准方程;
(2)已知点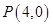 ,连接
,连接 与椭圆的另一交点记为
与椭圆的另一交点记为 ,若
,若 与椭圆相切时
与椭圆相切时 、
、 不重合,连接
不重合,连接 与椭圆的另一交点记为
与椭圆的另一交点记为 ,求
,求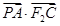 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市2013年发放汽车牌照12万张,其中燃油型汽车牌照10万张,电动型汽车2万张.为了节能减排和控制总量,从2013年开始,每年电动型汽车牌照按50%增长,而燃油型汽车牌照每一年比上一年减少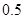 万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.
万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.
(1)记2013年为第一年,每年发放的燃油型汽车牌照数构成数列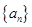 ,每年发放的电动型汽车牌照数为构成数列
,每年发放的电动型汽车牌照数为构成数列 ,完成下列表格,并写出这两个数列的通项公式;
,完成下列表格,并写出这两个数列的通项公式;
(2)从2013年算起,求二十年发放的汽车牌照总量.
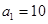 | 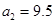 | 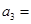 | 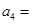 | |
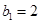 |  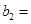 3 3 | 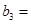 | 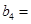 | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com