如图，制图工程师要用两个同中心的边长均为4的正方形合成一个八角形图形．由对称性，图中8个三角形都是全等的三角形，设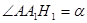
．
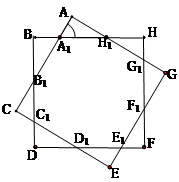
（1）试用
表示
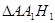的面积；
（2）求八角形所覆盖面积的最大值，并指出此时的大小．
科目：高中数学 来源： 题型：解答题
某单位有员工1000名，平均每人每年创造利润10万元。为了增加企业竞争力，决定优化产业结构，调整出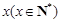
名员工从事第三产业，调整后他们平均每人每年创造利为
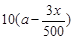万元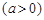
，剩下的员工平均每人每年创造的利润可以提高
.
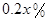（1）若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润，则最多调整出多少名员工从事第三产业？
（2）在（1）的条件下，若调整出的员工创造的年总利润始终不高于剩余员工创造的年总利润，则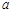
的取值范围是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
经过长期观测得到：在交通繁忙的时段内，某公路段汽车的车流量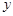
（千辆/时）与汽车的平均速度
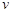（千米/时）之间的函数关系为
（
）．
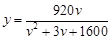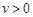（1）在该时段内，当汽车的平均速度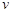为多少时，车流量最大？最大车流量为多少？
（2）若要求在该时段内车流量超过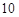
千辆/时，则汽车的平均速度应在什么范围内？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数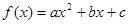
（a≠0）满足
，
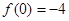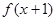为偶函数，且x＝－2是函数
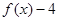的一个零点．又
（
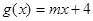＞0）．
（1）求函数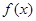
的解析式；
（2）若关于x 的方程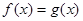
在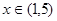
上有解，求实数的取值范围；
（3）令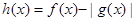
，求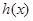
的单调区间．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知二次函数f(x)＝ax2＋bx＋c (a≠0)且满足f(－1)＝0，对任意实数x，恒有f(x)－x≥0，并且当x∈(0,2)时，f(x)≤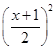
.
(1)求f(1)的值；
(2)证明：a>0，c>0；
(3)当x∈[－1,1]时，函数g(x)＝f(x)－mx (x∈R)是单调函数，求证：m≤0或m≥1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
,
,
则
，
；由
可得
；对于（2）换元法是解题常用方法，可以减少许多不必要的运算量，提高解题效率，注意换元前后的对等关系，令
代入面积表达式可得：
.
为
,∴
，
,
取到最大值的情况，即为
, 即
.
的定义域和值域均是
，求实数
的值；
上是减函数，且对任意的
，
，总有
，求实数
是
上的奇函数，且当
时，
.
且f(4)＝
.
__________.