
已知函数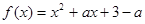 ,
,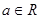 .
.
(1)求 的取值范围,使
的取值范围,使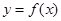 在闭区间
在闭区间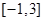 上是单调函数;
上是单调函数;
(2)当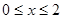 时,函数
时,函数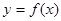 的最大值是关于
的最大值是关于 的函数
的函数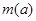 .求
.求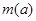 ;
;
(3)求实数 的取值范围,使得对任意的
的取值范围,使得对任意的
 ,恒有
,恒有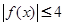 成立.
成立.
(1)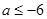 或
或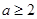 ;(2)
;(2) 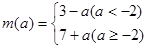 ;(3)
;(3)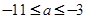 .
.
解析试题分析:(1)求出函数f(x)=x2+ax+3-a图象的对称轴为x=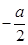 .由f(x)在闭区间[-1,3]上是单调函数,能够求出a的取值范围;(2)当a≥0时,m(a)=f(0)=3-a;当-4≤a<0时,m(a)=f(
.由f(x)在闭区间[-1,3]上是单调函数,能够求出a的取值范围;(2)当a≥0时,m(a)=f(0)=3-a;当-4≤a<0时,m(a)=f(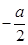 )=
)=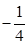 a2-a+3;当a<-4时,m(a)=f(2)=a+7.分段讨论并比较大小得,能够求出m(a)的最大值及;(3)将
a2-a+3;当a<-4时,m(a)=f(2)=a+7.分段讨论并比较大小得,能够求出m(a)的最大值及;(3)将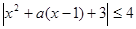 在
在
 时恒成立化成
时恒成立化成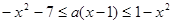 在
在
 时恒成立,分类讨论当
时恒成立,分类讨论当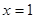 时显然成立,当
时显然成立,当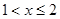 时,
时,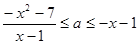 在
在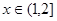 时恒成立,即可求出a的范围.
时恒成立,即可求出a的范围.
解:(1)函数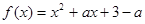 图像的对称轴为
图像的对称轴为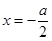 .
.
因为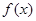 在闭区间
在闭区间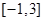 上是单调函数,所以
上是单调函数,所以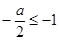 或
或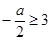 .
.
故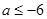 或
或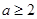 .
.
(2)当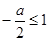 即
即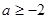 时
时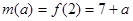
当 即
即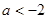 时
时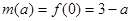
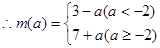
(3)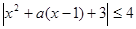 在
在
 时恒成立
时恒成立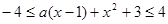 在
在
 时恒成立
时恒成立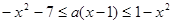 在
在
 时恒成立
时恒成立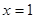 时显然成立
时显然成立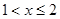 时,
时,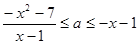 在
在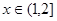 时恒成立
时恒成立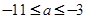 .
.
考点:1.二次函数的性质;2.二次函数在闭区间上的最值.


科目:高中数学 来源: 题型:解答题
已知函数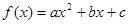 (a≠0)满足
(a≠0)满足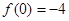 ,
,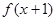 为偶函数,且x=-2是函数
为偶函数,且x=-2是函数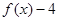 的一个零点.又
的一个零点.又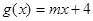 (
( >0).
>0).
(1)求函数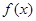 的解析式;
的解析式;
(2)若关于x 的方程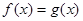 在
在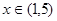 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
(3)令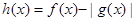 ,求
,求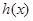 的单调区间.
的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数f(x)=ax2+bx+c (a≠0)且满足f(-1)=0,对任意实数x,恒有f(x)-x≥0,并且当x∈(0,2)时,f(x)≤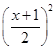 .
.
(1)求f(1)的值;
(2)证明:a>0,c>0;
(3)当x∈[-1,1]时,函数g(x)=f(x)-mx (x∈R)是单调函数,求证:m≤0或m≥1.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市2013年发放汽车牌照12万张,其中燃油型汽车牌照10万张,电动型汽车2万张.为了节能减排和控制总量,从2013年开始,每年电动型汽车牌照按50%增长,而燃油型汽车牌照每一年比上一年减少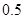 万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.
万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.
(1)记2013年为第一年,每年发放的燃油型汽车牌照数构成数列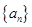 ,每年发放的电动型汽车牌照数为构成数列
,每年发放的电动型汽车牌照数为构成数列 ,完成下列表格,并写出这两个数列的通项公式;
,完成下列表格,并写出这两个数列的通项公式;
(2)从2013年算起,求二十年发放的汽车牌照总量.
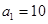 | 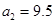 | 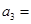 | 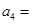 | |
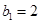 |  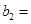 3 3 | 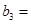 | 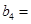 | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某公司以每吨10万元的价格销售某种产品,每年可售出该产品1000吨,若将该产品每吨的价格上涨x%,则每年的销售数量将减少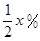 ,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校要建一个面积为450平方米的矩形球场,要求球场的一面利用旧墙,其他各面用钢筋网围成,且在矩形一边的钢筋网的正中间要留一个3米的进出口(如图).设矩形的长为 米,钢筋网的总长度为
米,钢筋网的总长度为 米.
米.
(1)列出 与
与 的函数关系式,并写出其定义域;
的函数关系式,并写出其定义域;
(2)问矩形的长与宽各为多少米时,所用的钢筋网的总长度最小?
(3)若由于地形限制,该球场的长和宽都不能超过25米,问矩形的长与宽各为多少米时,所用的钢筋网的总长度最小?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地方政府在某地建一座桥,两端的桥墩相距m米,此工程只需建两端桥墩之间的桥面和桥墩(包括两端的桥墩).经预测,一个桥墩的费用为256万元,相邻两个桥墩之间的距离均为x,且相邻两个桥墩之间的桥面工程费用为(1+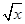 )x万元,假设所有桥墩都视为点且不考虑其他因素,记工程总费用为y万元.
)x万元,假设所有桥墩都视为点且不考虑其他因素,记工程总费用为y万元.
(1)试写出y关于x的函数关系式;
(2)当m=1280米时,需要新建多少个桥墩才能使y最小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com