某地方政府在某地建一座桥，两端的桥墩相距m米，此工程只需建两端桥墩之间的桥面和桥墩(包括两端的桥墩)．经预测，一个桥墩的费用为256万元，相邻两个桥墩之间的距离均为x，且相邻两个桥墩之间的桥面工程费用为(1＋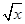
)x万元，假设所有桥墩都视为点且不考虑其他因素，记工程总费用为y万元．
(1)试写出y关于x的函数关系式；
(2)当m＝1280米时，需要新建多少个桥墩才能使y最小？
全优考典单元检测卷及归类总复习系列答案科目：高中数学 来源： 题型：解答题
已知函数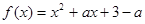
，
.
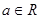（1）求
的取值范围，使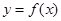
在闭区间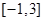
上是单调函数；
（2）当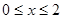
时，函数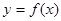
的最大值是关于的函数
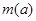.求；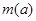
（3）求实数的取值范围，使得对任意的
，恒有
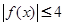成立.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
经市场调查，某种商品在过去50天的销量和价格均为销售时间t(天)的函数，且销售量近似地满足f(t)＝－2t＋200(1≤t≤50，t∈N)，前30天价格为g(t)＝
t＋30(1≤t≤30，t∈N)，后20天价格为g(t)＝45(31≤t≤50，t∈N)．
(1)写出该种商品的日销售额S与时间t的函数关系式；
(2)求日销售额S的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知关于x的二次方程x2＋2mx＋2m＋1＝0.
(1)若方程有两根，其中一根在区间(－1，0)内，另一根在区间(1，2)内，求实数m的取值范围；
(2)若方程两根均在区间(0，1)内，求实数m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数f(x)＝x2－4，设曲线y＝f(x)在点(xn，f(xn))
处的切线与x轴的交点为(xn＋1,0)(n∈N＋)，其中x1为正实数．
(1)用xn表示xn＋1；
(2)求证：对一切正整数n，xn＋1≤xn的充要条件是x1≥2；
(3)若x1＝4，记an＝lg 
，证明数列{an}成等比数列，并求数列{xn}的通项公式．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数f(x)＝log4(4x＋1)＋kx(k∈R)为偶函数．
(1)求k的值；
(2)若方程f(x)＝log4(a·2x－a)有且只有一个根，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知两条直线l1：y＝m和l2：y＝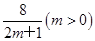
，l1与函数y＝|log2x|的图象从左至右相交于点A、B，l2与函数y＝|log2x|的图象从左至右相交于点C、D.记线段AC和BD在x轴上的投影长度分别为a、b.当m变化时，求
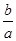的最小值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
＋m＋256 
（2）21
．
内的任意
，总有
成立，求实数
的取值范围；
在区间
内有两个不同的零点
，求：
的取值范围．
的值．