
科目:高中数学 来源: 题型:解答题
某市2013年发放汽车牌照12万张,其中燃油型汽车牌照10万张,电动型汽车2万张.为了节能减排和控制总量,从2013年开始,每年电动型汽车牌照按50%增长,而燃油型汽车牌照每一年比上一年减少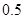 万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.
万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.
(1)记2013年为第一年,每年发放的燃油型汽车牌照数构成数列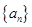 ,每年发放的电动型汽车牌照数为构成数列
,每年发放的电动型汽车牌照数为构成数列 ,完成下列表格,并写出这两个数列的通项公式;
,完成下列表格,并写出这两个数列的通项公式;
(2)从2013年算起,求二十年发放的汽车牌照总量.
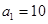 | 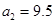 | 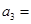 | 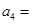 | |
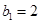 |  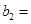 3 3 | 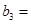 | 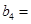 | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数.
(1)求k的值;
(2)设g(x)=log4 ,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
,若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地方政府在某地建一座桥,两端的桥墩相距m米,此工程只需建两端桥墩之间的桥面和桥墩(包括两端的桥墩).经预测,一个桥墩的费用为256万元,相邻两个桥墩之间的距离均为x,且相邻两个桥墩之间的桥面工程费用为(1+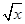 )x万元,假设所有桥墩都视为点且不考虑其他因素,记工程总费用为y万元.
)x万元,假设所有桥墩都视为点且不考虑其他因素,记工程总费用为y万元.
(1)试写出y关于x的函数关系式;
(2)当m=1280米时,需要新建多少个桥墩才能使y最小?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知幂函数y=x3m-9(m∈N*)的图象关于y轴对称,且在(0,+∞)上是减函数.
(1)求m的值;
(2)求满足不等式(a+1)-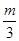 <(3-2a)-
<(3-2a)-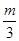 的实数a的取值范围.
的实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=x2+mx+n的图象过点(1,3),且f(-1+x)=f(-1-x)对任意实数都成立,函数y=g(x)与y=f(x)的图象关于原点对称.
(1)求f(x)与g(x)的解析式;
(2)若F(x)=g(x)-λf(x)在(-1,1]上是增函数,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=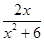 .
.
(1)若f(x)>k的解集为{x|x<-3,或x>-2},求k的值;
(2)对任意x>0,f(x)≤t恒成立,求t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com