已知函数f(x)＝log4(4x＋1)＋kx(k∈R)为偶函数．
(1)求k的值；
(2)若方程f(x)＝log4(a·2x－a)有且只有一个根，求实数a的取值范围．
口算能手系列答案科目：高中数学 来源： 题型：解答题
某地方政府在某地建一座桥，两端的桥墩相距m米，此工程只需建两端桥墩之间的桥面和桥墩(包括两端的桥墩)．经预测，一个桥墩的费用为256万元，相邻两个桥墩之间的距离均为x，且相邻两个桥墩之间的桥面工程费用为(1＋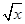
)x万元，假设所有桥墩都视为点且不考虑其他因素，记工程总费用为y万元．
(1)试写出y关于x的函数关系式；
(2)当m＝1280米时，需要新建多少个桥墩才能使y最小？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
设函数f(x)＝ax2＋bx＋b－1(a≠0)．
(1)当a＝1，b＝－2时，求函数f(x)的零点；
(2)若对任意b∈R，函数f(x)恒有两个不同零点，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知二次函数f(x)的二次项系数为a，且不等式f(x)＞2x的解集为(－1,3)．
(1)若函数g(x)＝xf(x)在区间
内单调递减，求a的取值范围；
(2)当a＝－1时，证明方程f(x)＝2x3－1仅有一个实数根；
(3)当x∈[0,1]时，试讨论|f(x)＋(2a－1)x＋3a＋1|≤3成立的充要条件．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数f(x)＝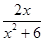
.
(1)若f(x)>k的解集为{x|x<－3，或x>－2}，求k的值；
(2)对任意x>0，f(x)≤t恒成立，求t的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
设
,
.
（Ⅰ）证明：
；
（Ⅱ）求证：在数轴上，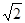
介于
与
之间，且距较远；
（Ⅲ）在数轴上，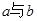
之间的距离是否可能为整数？若有，则求出这个整数；若没有，
说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数f(x)＝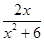
.
(1)若f(x)>k的解集为{x|x<－3，或x>－2}，求k的值；
(2)对任意x>0，f(x)≤t恒成立，求t的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
(2) a的取值范围为{a|a>1或a＝－2－2
}
，
.
在
上不具有单调性，求实数
的取值范围； 
.
的值；
，
，
，当
时，试比较
，
，
的大小．