已知函数f(x)的图象与函数h(x)＝x＋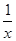
＋2的图象关于点A(0,1)对称．
(1)求f(x)的解析式；
(2)若g(x)＝f(x)·x＋ax，且g(x)在区间[0,2]上为减函数，求实数a的取值范围．
科目：高中数学 来源： 题型：解答题
（12分）（2011•湖北）提高过江大桥的车辆通行能力可改善整个城市的交通状况，在一般情况下，大桥上的车流速度v（单位：千米/小时）是车流密度x（单位：辆/千米）的函数，当桥上的车流密度达到200辆/千米时，造成堵塞，此时车流速度为0；当车流密度不超过20辆/千米时，车流速度为60千米/小时，研究表明：当20≤x≤200时，车流速度v是车流密度x的一次函数．
（Ⅰ）当0≤x≤200时，求函数v（x）的表达式；
（Ⅱ）当车流密度x为多大时，车流量（单位时间内通过桥上某观测点的车辆数，单位：辆/小时）f（x）=x•v（x）可以达到最大，并求出最大值．（精确到1辆/小时）．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知二次函数f(x)＝ax2＋bx＋c (a≠0)且满足f(－1)＝0，对任意实数x，恒有f(x)－x≥0，并且当x∈(0,2)时，f(x)≤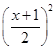
.
(1)求f(1)的值；
(2)证明：a>0，c>0；
(3)当x∈[－1,1]时，函数g(x)＝f(x)－mx (x∈R)是单调函数，求证：m≤0或m≥1.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
某公司以每吨10万元的价格销售某种产品，每年可售出该产品1000吨，若将该产品每吨的价格上涨x%，则每年的销售数量将减少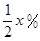
，该产品每吨的价格上涨百分之几，可使销售的总金额最大？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
市场营销人员对过去几年某商品的价格及销售数量的关系作数据分析发现有如下规律：该商品的价格每上涨x%(x>0)，销售数量就减少kx%(其中k为正常数)．目前该商品定价为每个a元，统计其销售数量为b个．
(1)当k＝
时，该商品的价格上涨多少，才能使销售的总金额达到最大？
(2)在适当的涨价过程中，求使销售总金额不断增加时k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
是
上的奇函数，且当
时，
.
定义在
上，对任意的
，
，且
.
，并证明：
；
.设向量
，对任意
，
恒成立，求实数
的取值范围.
都是实数，且
．
的解集；
对满足条件的所有实数
的取值范围．
的前
项和
，数列
满足
．
．