
某渔业公司年初用49万元购买一艘捕鱼船,第一年各种费用6万元,以后每年都增加2万元,每年捕鱼收益25万元.
(1)问第几年开始获利?
(2)若干年后,有两种处理方案:①年平均获利最大时,以18万元出售该渔船;②总纯收入获利最大时,以9万元出售该渔船.问哪种方案最合算?
(1)渔业公司第3年开始获利.(2)方案①较合算.
解析试题分析:(1)由题意列出获利y与年份n的函数关系,然后求解不等式得到n的范围,根据n是正的自然数求得n的值;
(2)用获利除以年份得到年平均获利,利用不等式求出最大值,求出获得的总利润,利用配方法求出获得利润的最大值,求出总获利,比较后即可得到答案.
试题解析:(1)第n年开始获利,设获利为y万元,则
y=25n-[6n+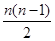 ×2]-49=-n2+20n-49 2分
×2]-49=-n2+20n-49 2分
由y=-n2+20n-49>0得10-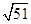 <n<10+
<n<10+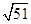 4分
4分
又∵n∈N*,∴n=3,4
∴n=3时,即该渔业公司第3年开始获利. 5分
(2)方案①:年平均获利为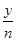 =-n-
=-n- +20≤-2
+20≤-2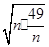 +20=6(万元) 7分
+20=6(万元) 7分
当n=7时,年平均获利最大,若此时卖出,共获利6×7+18=60(万元) 8分
方案②:y=-n2+20n-49=-(n-10)2+51
当且仅当n=10时,即该渔业公司第10年总额最大,若此时卖出,共获利51+9=60万元 11分
因为两种方案获利相等,但方案②所需的时间长,所以方案①较合算. 12分
考点:函数模型的选择及应用;简单的建模思想;利用基本不等式求最值;配方法.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:解答题
某种商品,现在定价p元,每月卖出n件,设定价上涨x成,每月卖出数量减少y成,每月售货总金额变成现在的z倍.
(1)用x和y表示z;
(2)设x与y满足y=kx(0<k<1),利用k表示当每月售货总金额最大时x的值;
(3)若y= x,求使每月售货总金额有所增加的x值的范围.
x,求使每月售货总金额有所增加的x值的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对于函数 ,若存在实数对(
,若存在实数对( ),使得等式
),使得等式 对定义域中的每一个
对定义域中的每一个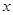 都成立,则称函数
都成立,则称函数 是“(
是“( )型函数”.
)型函数”.
(1) 判断函数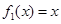 是否为 “(
是否为 “( )型函数”,并说明理由;
)型函数”,并说明理由;
(2) 若函数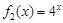 是“(
是“( )型函数”,求出满足条件的一组实数对
)型函数”,求出满足条件的一组实数对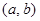 ;
;
(3)已知函数 是“
是“ 型函数”,对应的实数对
型函数”,对应的实数对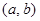 为
为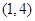 ,当
,当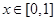 时,
时,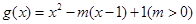 ,若当
,若当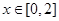 时,都有
时,都有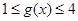 ,试求
,试求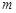 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
用总长为14.8m的钢条制作一个长方体容器的框架,如果所制作容器的底面的一边比另一边长0.5m,那么高为多少时容器的容积最大?并求出它的最大容积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知定义域为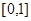 的函数
的函数 同时满足以下三个条件:
同时满足以下三个条件:
①对任意的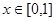 ,总有
,总有 ;
;
②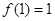 ;
;
③当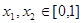 ,且
,且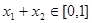 时,
时,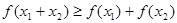 成立.
成立.
称这样的函数为“友谊函数”.
请解答下列各题:
(1)已知 为“友谊函数”,求
为“友谊函数”,求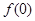 的值;
的值;
(2)函数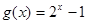 在区间
在区间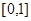 上是否为“友谊函数”?请给出理由;
上是否为“友谊函数”?请给出理由;
(3)已知 为“友谊函数”,假定存在
为“友谊函数”,假定存在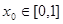 ,使得
,使得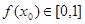 ,且
,且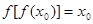 ,求证:
,求证: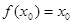 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某公司为一家制冷设备厂设计生产一种长方形薄板,其周长为4米,这种薄板须沿其对角线折叠后使用.如图所示,ABCD(AB>AD)为长方形薄板,沿AC折叠后,AB′交DC于点P.当△ADP的面积最大时最节能,凹多边形ACB′PD的面积最大时制冷效果最好.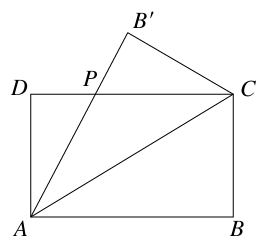
(1)设AB=x(米),用x表示图中DP的长度,并写出x的取值范围;
(2)若要求最节能,应怎样设计薄板的长和宽?
(3)若要求制冷效果最好,应怎样设计薄板的长和宽?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知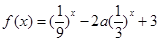
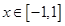
(1)若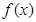 的最小值记为
的最小值记为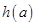 ,求
,求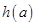 的解析式.
的解析式.
(2)是否存在实数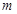 ,
,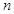 同时满足以下条件:①
同时满足以下条件:① ;②当
;②当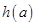 的定义域为[
的定义域为[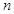 ,
,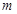 ]时,值域为[
]时,值域为[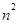 ,
,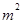 ];若存在,求出
];若存在,求出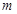 ,
,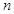 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com