
已知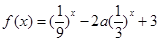
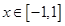
(1)若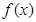 的最小值记为
的最小值记为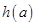 ,求
,求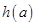 的解析式.
的解析式.
(2)是否存在实数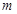 ,
,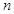 同时满足以下条件:①
同时满足以下条件:① ;②当
;②当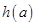 的定义域为[
的定义域为[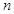 ,
,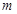 ]时,值域为[
]时,值域为[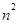 ,
,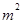 ];若存在,求出
];若存在,求出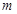 ,
,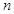 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(1) 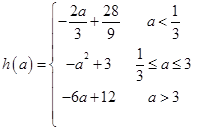 ;(2) 满足条件的实数m,n不存在.
;(2) 满足条件的实数m,n不存在.
解析试题分析:(1)利用换元法令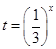 ,可知
,可知 ,原函数化为
,原函数化为 ,利用一元二次函数求最值,可得最小值
,利用一元二次函数求最值,可得最小值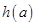 的解析式;(2)由 ①知m>n>3,故
的解析式;(2)由 ①知m>n>3,故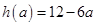 ,由函数的单调性知
,由函数的单调性知
12?6m=n2,12?6n=m2 得m+n=6与m>n>3矛盾,故不存在.
解:(1)令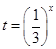 ,∵
,∵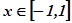 ∴
∴ , 1分
, 1分
 ,对称轴
,对称轴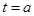 . 2分
. 2分
①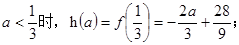
②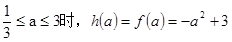 ,
,
③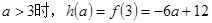 , 5分
, 5分
∴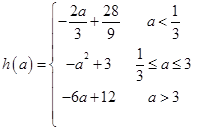 7分
7分
(2)因为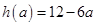 在(3,+∞)上为减函数,而m>n>3,
在(3,+∞)上为减函数,而m>n>3,
∴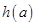 在[n,m]上的值域为[h(m),h(n)], (8分)
在[n,m]上的值域为[h(m),h(n)], (8分)
∵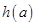 在[n,m]上的值域为[
在[n,m]上的值域为[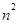 ,
,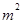 ],
],
∴h(m)=n2, h(n)=m2
即:12?6m=n2 ,12?6n=m2 (9分)
两式相减得:6(m-n)=(m-n)(m+n)
又m>n>3∴m+n=6,而m>n>3时,有m+n>6,矛盾. (12分)
故满足条件的实数m,n不存在. (13分)
考点:换元法,一元二次函数的最值,函数的单调性.


科目:高中数学 来源: 题型:解答题
某渔业公司年初用49万元购买一艘捕鱼船,第一年各种费用6万元,以后每年都增加2万元,每年捕鱼收益25万元.
(1)问第几年开始获利?
(2)若干年后,有两种处理方案:①年平均获利最大时,以18万元出售该渔船;②总纯收入获利最大时,以9万元出售该渔船.问哪种方案最合算?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分)本题共有2个小题,第1小题满分6分,第2个小题满分8分。
某加油站拟造如图所示的铁皮储油罐(不计厚度,长度单位:米),其中储油罐的中间为圆柱形,左右两端均为半球形,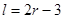 (
(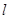 为圆柱的高,
为圆柱的高,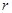 为球的半径,
为球的半径,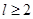 ).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为
).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为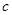 千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为
千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为 千元.
千元.
(1)写出 关于
关于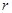 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(2)求该储油罐的建造费用最小时的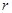 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=lnx+a ,其中a为大于零的常数.
,其中a为大于零的常数.
(1)若函数f(x)在区间[1,+∞)内单调递增,求实数a的取值范围.
(2)求证:对于任意的n∈N*,且n>1时,都有lnn> +
+ +…+
+…+ 恒成立.
恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某造纸厂拟建一座底面图形为矩形且面积为162平方米的三级污水处理池,池的深度一定(平面图如图所示),如果池四周围墙建造单价为400元/米,中间两道隔墙建造单价为248元/米,池底建造单价为80元/平方米,水池所有墙的厚度忽略不计.
(1)试设计污水处理池的长和宽,使总造价最低,并求出最低总造价;
(2)若由于地形限制,该池的长和宽都不能超过16米,试设计污水处理池的长和宽,使总造价最低,并求出最低总造价.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2014·郑州模拟)已知函数f(x)=ex+ax,g(x)=ax-lnx,其中a≤0.
(1)求f(x)的极值.
(2)若存在区间M,使f(x)和g(x)在区间M上具有相同的单调性,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某森林出现火灾,火势正以100m2/分钟的速度顺风蔓延,消防站接到报警立即派消防队员前去,在火灾发生后5分钟到达救火现场,已知消防队员在现场平均每人灭火50m2/分钟,所消耗的灭火材料,劳务津贴等费用为人均125元/分钟,另附加每次救火所耗损的车辆、器械和装备等费用人均100元,而烧毁森林的损失费60元/m2,应该派多少消防队员前去救火才能使总损失最少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数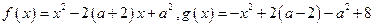 .设
.设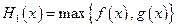 ,
,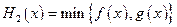 (max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记
(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记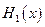 的最小值为A,
的最小值为A,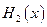 的最大值为B,则
的最大值为B,则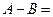 ( )
( )
| A.16 |
B.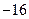 |
C.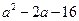 |
D.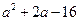 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com