
已知函数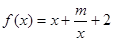 (
(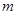 为实常数).
为实常数).
(1)若函数 在区间
在区间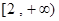 上是增函数,试用函数单调性的定义求实数
上是增函数,试用函数单调性的定义求实数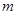 的取值范围;
的取值范围;
(2)设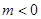 ,若不等式
,若不等式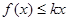 在
在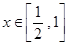 有解,求
有解,求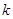 的取值范围.
的取值范围.
(1)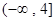 ;(2)当
;(2)当 时,
时,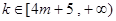 ;当
;当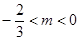 时,
时,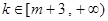 .
.
解析试题分析:(1)任取x1、x2∈[2,+∞),且x1<x2,利用函数单调性的定义可知f(x2)-f(x1)>0在区间[2,+∞)上恒成立,从而求出实数m的取值范围;(2)将不等式f(x)≤kx中的k分离出来,然后利用二次函数的性质研究不等式另一侧函数在[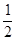 ,1]上的最小值,从而求出k的取值范围.
,1]上的最小值,从而求出k的取值范围.
(1)由题意,任取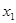 、
、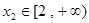 ,且
,且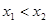 ,
,
则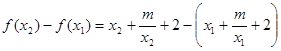
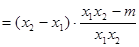
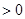 , 2分
, 2分
因为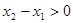 ,
,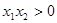 ,所以
,所以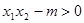 ,即
,即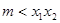 , 4分
, 4分
由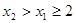 ,得
,得 ,所以
,所以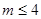 .所以,
.所以,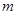 的取值范围是
的取值范围是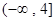 . 6分
. 6分
(2)由 ,得
,得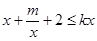 ,
,
因为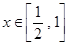 ,所以
,所以 , 7分
, 7分
令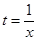 ,则
,则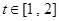 ,所以
,所以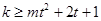 ,令
,令 ,
,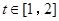 ,
,
于是,要使原不等式在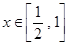 有解,当且仅当
有解,当且仅当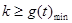 (
(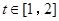 ). 9分
). 9分
因为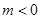 ,所以
,所以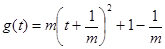 图像开口向下,对称轴为直线
图像开口向下,对称轴为直线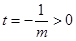 ,
,
因为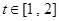 ,故当
,故当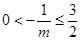 ,即
,即 时,
时, ;
;
当 ,即
,即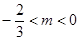 时,
时,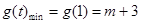 . 13分
. 13分
综上,当 时,
时,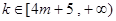 ;
;
当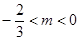 时,
时,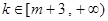 . 14分.
. 14分.
考点:1.不等式的解法;2.奇偶性与单调性的综合;3.两点间的距离公式..


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:解答题
设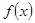 是定义在
是定义在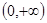 上的函数,且
上的函数,且 ,对任意
,对任意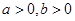 ,若经过点
,若经过点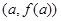 ,
,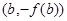 的直线与
的直线与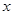 轴的交点为
轴的交点为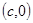 ,则称
,则称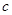 为
为 关于函数
关于函数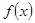 的平均数,记为
的平均数,记为 ,例如,当
,例如,当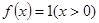 时,可得
时,可得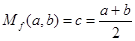 ,即
,即 为
为 的算术平均数.
的算术平均数.
当 时,
时, 为
为 的几何平均数;
的几何平均数;
当 时,
时, 为
为 的调和平均数
的调和平均数 ;
;
(以上两空各只需写出一个符合要求的函数即可)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分)本题共有2个小题,第1小题满分6分,第2个小题满分8分。
某加油站拟造如图所示的铁皮储油罐(不计厚度,长度单位:米),其中储油罐的中间为圆柱形,左右两端均为半球形,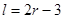 (
(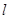 为圆柱的高,
为圆柱的高,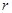 为球的半径,
为球的半径,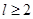 ).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为
).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为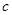 千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为
千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为 千元.
千元.
(1)写出 关于
关于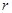 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(2)求该储油罐的建造费用最小时的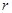 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某造纸厂拟建一座底面图形为矩形且面积为162平方米的三级污水处理池,池的深度一定(平面图如图所示),如果池四周围墙建造单价为400元/米,中间两道隔墙建造单价为248元/米,池底建造单价为80元/平方米,水池所有墙的厚度忽略不计.
(1)试设计污水处理池的长和宽,使总造价最低,并求出最低总造价;
(2)若由于地形限制,该池的长和宽都不能超过16米,试设计污水处理池的长和宽,使总造价最低,并求出最低总造价.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2014·郑州模拟)已知函数f(x)=ex+ax,g(x)=ax-lnx,其中a≤0.
(1)求f(x)的极值.
(2)若存在区间M,使f(x)和g(x)在区间M上具有相同的单调性,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,长方形物体E在雨中沿面P(面积为S)的垂直方向作匀速移动,速度为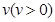 ,雨速沿E移动方向的分速度为
,雨速沿E移动方向的分速度为 。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与
。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与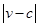 ×S成正比,比例系数为
×S成正比,比例系数为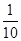 ;(2)其它面的淋雨量之和,其值为
;(2)其它面的淋雨量之和,其值为 ,记
,记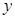 为E移动过程中的总淋雨量,当移动距离d=100,面积S=
为E移动过程中的总淋雨量,当移动距离d=100,面积S=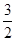 时。
时。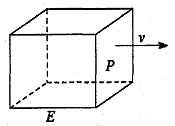
(1)写出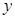 的表达式
的表达式
(2)设0<v≤10,0<c≤5,试根据c的不同取值范围,确定移动速度 ,使总淋雨量
,使总淋雨量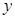 最少。
最少。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
据市场分析,广饶县驰中集团某蔬菜加工点,当月产量在10吨至25吨时,月生产总成本 (万元)可以看成月产量
(万元)可以看成月产量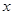 (吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(1)写出月总成本 (万元)关于月产量
(万元)关于月产量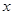 (吨)的函数关系;
(吨)的函数关系;
(2)已知该产品销售价为每吨1.6万元,那么月产量为多少时,可获最大利润;
(3)当月产量为多少吨时, 每吨平均成本最低,最低成本是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数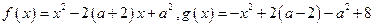 .设
.设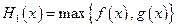 ,
,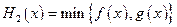 (max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记
(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记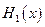 的最小值为A,
的最小值为A,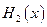 的最大值为B,则
的最大值为B,则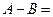 ( )
( )
| A.16 |
B.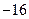 |
C.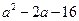 |
D.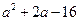 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com