

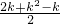
 =Ck+10+Ck+1k+Ck+12,结论也成立,由①②知,n条直线将一个平面最多分成Cn0+Cn1+Cn2个部分(n>1).
=Ck+10+Ck+1k+Ck+12,结论也成立,由①②知,n条直线将一个平面最多分成Cn0+Cn1+Cn2个部分(n>1).

科目:高中数学 来源:学习周报 数学 北师大课标高二版(选修1-2) 2009-2010学年 第39期 总第195期 北师大课标 题型:044
一个平面用n条直线去划分,最多将平面分成f(n)个部分.
(1)求f(1),f(2),f(3),f(4);
(2)观察f(2)-f(1),f(3)-f(2),f(4)-f(3)有何规律;
(3)求出f(n).
查看答案和解析>>
科目:高中数学 来源:2012年苏教版高中数学选修1-2 2.1合情推理与演绎推理练习卷(解析版) 题型:解答题
一个平面用n条直线去划分,最多将平面分成 个部分.
个部分.
(1)求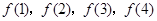 ;
;
(2)观察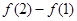 ,
,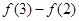 ,
, 有何规律;
有何规律;
(3)求出
查看答案和解析>>
科目:高中数学 来源:江苏省2010年高考预测试题数学 题型:解答题
2条直线将一个平面最多分成4部分,3条直线将一个平面最多分成7部分, 4条直线将一个平面最多分成11部分,……;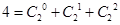 ,
, ,
,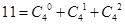 ;……
;……
(1)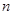 条直线将一个平面最多分成多少个部分(
条直线将一个平面最多分成多少个部分(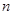 >1)?证明你的结论;
>1)?证明你的结论;
(2)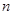 个平面最多将空间分割成多少个部分(
个平面最多将空间分割成多少个部分(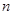 >2)?证明你的结论
>2)?证明你的结论
查看答案和解析>>
科目:高中数学 来源:2010年山西省忻州市高二下学期期末联考(文科)数学卷 题型:解答题
(本题满分10分)
一个平面用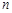 条直线去划分,最多将平面分成
条直线去划分,最多将平面分成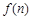 个部分.
个部分.
(1)求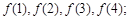
(2)观察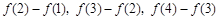 有何规律,用含
有何规律,用含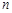 的式子表示(不必证明);
的式子表示(不必证明);
(3)求出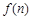 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com