
分析 (1)由正切函数的定义域可得$\frac{x}{2}+\frac{π}{3}≠\frac{π}{2}+kπ$,求得x的范围得答案;
(2)由根式内部的代数式大于等于0,求解三角不等式得答案.
解答 解:(1)由$\frac{x}{2}+\frac{π}{3}≠\frac{π}{2}+kπ$,得x≠$\frac{π}{3}+2kπ$,k∈Z.
∴函数$f(x)=tan(\frac{x}{2}+\frac{π}{3})$的定义域为{x|x≠$\frac{π}{3}+2kπ$,k∈Z};
(2)由2sinx-1≥0,得sinx$≥\frac{1}{2}$,
∴$\frac{π}{6}+2kπ≤x≤\frac{5π}{6}+2kπ$,k∈Z.
∴函数$f(x)=\sqrt{2sinx-1}$的定义域为[$\frac{π}{6}+2kπ,\frac{5π}{6}+2kπ$],k∈Z.
点评 本题考查函数的定义域及其求法,考查了三角不等式的解法,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
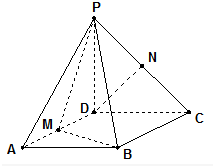 如图,在四棱锥P-ABCD中,底面ABCD是以∠A=60°的菱形,PD⊥底面ABCD,且PD=CD,点M,N分别为棱AD,PC的中点证明:
如图,在四棱锥P-ABCD中,底面ABCD是以∠A=60°的菱形,PD⊥底面ABCD,且PD=CD,点M,N分别为棱AD,PC的中点证明:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M一定在直线AC上 | B. | M一定在直线CD上 | ||
| C. | M可能在AC上,也可能在BD上 | D. | M不在AC上,也不在BD上 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ab>b2 | B. | ($\frac{1}{2}$)a<($\frac{1}{2}$)b | ||
| C. | log${\;}_{\frac{1}{2}}$a>log${\;}_{\frac{1}{2}}$b | D. | a2>b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com