
分析 先根据二次函数的解析式分别研究分段函数在各自区间上的单调性,从而得到函数f(x)的单调性,由此性质转化求解不等式,解出参数范围即可.
解答 解:函数f(x),当x≥0 时,f(x)=x2+4x,由二次函数的性质知,它在[0,+∞)上是增函数,
当x<0时,f(x)=4x-x2,由二次函数的性质知,它在(-∞,0)上是增函数,
该函数连续,则函数f(x) 是定义在R 上的增函数
∵f(2-a)>f(4+3a),
∴2-a>4+3a
解得a<-$\frac{1}{2}$,
实数a 的取值范围是(-∞,-$\frac{1}{2}$)
故答案为:(-∞,-$\frac{1}{2}$)
点评 本题是奇偶性与单调性结合的一类最主要的题型,利用单调性将不等式f(2-a)>f(4+3a)转化为一元二次不等式,求出实数a 的取值范围,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
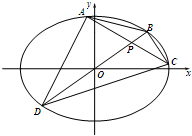 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的两焦点坐标为$({-\sqrt{2},0}),({\sqrt{2},0})$,且过点$({\sqrt{2},1})$.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的两焦点坐标为$({-\sqrt{2},0}),({\sqrt{2},0})$,且过点$({\sqrt{2},1})$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com