练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数.

    (1) 求函数的定义域；    

    (2) 判断函数在定义域上的单调性，并说明理由；

    （3）当满足什么关系时，在上恒取正值。

    解析：（1）要意义，-----------2分
    （只要学生得出答案，没有过程的，倒扣一分，用指数函数单调性或者直接解出）

    所求定义域为-----------------------------------------4分

    （2）函数在定义域上是单调递增函数------------------------------5分

    证明：---------------------------------------6分

    -----------------------------------------7分

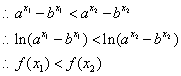    -----------------------------------9分

    所以原函数在定义域上是单调递增函数-------------------------10分

    （3）要使在上恒取正值

    须在上的最小值大于0--------------------------11分

    由（2）------------------------------12分

    所以在上恒取正值时有-------------------14分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数y=
    1+sinx3+cosx
    ，则该函数的值域是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数y=
    		1-x
    2x2-3x-2
    的定义域为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数(x-1)f(
    x+1x-1
    )+f(x)=x    ，其中x≠1，求函数解析式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2007•崇明县一模）已知函数y=-
    		1-x2
    （-1≤x≤0）的反函数是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2008•黄浦区一模）已知函数y=
    1+bx
    ax+1
    (a＞0，x≠-
    1
    a
    )    的图象关于直线y=x对称．
    （1）求实数b的值；
    （2）设A、B是函数图象上两个不同的定点，记向量
    e1
    =
    AB
    ，
    e2
    =(1，0)    ，试证明对于函数图象所在的平面里任一向量
    c
    ，都存在唯一的实数λ1、λ2，使得
    c
    =λ1
    e1
    +λ2
    e2
    成立．

    查看答案和解析>>

    同步练习册答案