
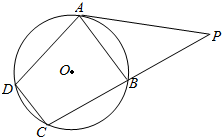
 如图,已知四边形ABCD是⊙O的内接四边形,过点A的切线与CB的延长线交于点P,且$PA=8\sqrt{2}$,PB=8.
如图,已知四边形ABCD是⊙O的内接四边形,过点A的切线与CB的延长线交于点P,且$PA=8\sqrt{2}$,PB=8.分析 (1)利用余弦定理可得AB,可得∠ABC=90°,再利用圆的内接四边形的性质即可得出;
(2)连接OC,作OM⊥BC于M,由垂径定理可知:M为BC的中点,利用切割线定理与勾股定理即可得出.
解答 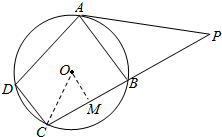 解:(1)在△PAB中,有$PA=8\sqrt{2}$,PB=8,∠APB=45°.
解:(1)在△PAB中,有$PA=8\sqrt{2}$,PB=8,∠APB=45°.
由余弦定理得:$A{B}^{2}={8}^{2}+(8\sqrt{2})^{2}-2×8×8\sqrt{2}cos4{5}^{°}$=64,解得AB=8.
∴AB=PB,∠BAP=45°,
∴∠ABP=Rt∠.
所以△PAB为Rt△,即AB⊥PC.
所以∠ABC=90°,
又因为四边形ABCD是⊙O的内接四边形,
所以∠D=90°.
(2)连接OC,作OM⊥BC于M,
由垂径定理可知:M为BC的中点,
由切割线定理得:PA2=PB•PC,
又$PA=8\sqrt{2}$,PB=8,
所以PC=16,BC=8,MC=4.
因为⊙O的半径为5,所以在Rt△OMT中有,OM=3,
所求圆心O到直线BC的距离为3.
点评 本题考查了余弦定理、圆的内接四边形的性质、垂径定理、切割线定理与勾股定理,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | c<b<a | C. | c<a<b | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 每个70元 | B. | 每个85元 | C. | 每个80元 | D. | 每个75元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com