
分析 (1)容易求出|x+2|+|x-3|的最小值为5,而根据不等式|x+2|+|x-3|<a的解集非空便知该不等式有解,从而有5<a,这样即求出实数a的取值范围;
(2)根据上面知|x+2|+|x-3|的最小值为5,而不等式|x+2|+|x-3|≥a恒成立,从而有5≥a,这即得出了实数a的取值范围.
解答 解:(1)根据条件知不等式|x+2|+|x-3|<a有解;
|x+2|+|x-3|≥|(x+2)-(x-3)|=5;
即|x+2|+|x-3|的最小值为5;
∴5<a;
即a>5;
∴实数a的取值范围为(5,+∞);
(2)|x+2|+|x-3|的最小值为5,且不等式|x+2|+|x-3|≥a恒成立;
∴5≥a;
即a≤5;
∴实数a的取值范围为(-∞,5].
点评 考查绝对值不等式公式:|a|+|b|≥|a-b|,清楚当不等式有解和不等式恒成立时求参数的取值范围的方法的不同.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 8 | C. | 6 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | -32 | C. | -33 | D. | -31 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
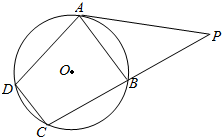 如图,已知四边形ABCD是⊙O的内接四边形,过点A的切线与CB的延长线交于点P,且$PA=8\sqrt{2}$,PB=8.
如图,已知四边形ABCD是⊙O的内接四边形,过点A的切线与CB的延长线交于点P,且$PA=8\sqrt{2}$,PB=8.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com