
【题目】已知椭圆C:![]() 的长轴是短轴的两倍,点
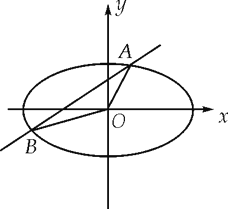
的长轴是短轴的两倍,点![]() 在椭圆上.不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为
在椭圆上.不过原点的直线l与椭圆相交于A、B两点,设直线OA、l、OB的斜率分别为![]() 、
、![]() 、
、![]() ,且
,且![]() 、
、![]() 、
、![]() 恰好构成等比数列.
恰好构成等比数列.
(Ⅰ)求椭圆C的方程.
(Ⅱ)试探究![]() 是否为定值?若是,求出这个值;否 则求出它的取值范围.
是否为定值?若是,求出这个值;否 则求出它的取值范围.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某班随机抽查了20名学生的数学成绩,分数制成如图的茎叶图,其中A组学生每天学习数学时间不足1个小时,B组学生每天学习数学时间达到一个小时。学校规定90分及90分以上记为优秀,75分及75分以上记为达标,75分以下记为未达标.

(1)分别求出A、B两组学生的平均分![]() 、
、![]() 并估计全班的数学平均分
并估计全班的数学平均分![]() ;
;
(2)现在从成绩优秀的学生中任意抽取2人,求这两人恰好都来自B组的概率;
(3)根据成绩得到如下列联表:

①直接写出表中![]() 的值;
的值;
②判断是否有![]() 的把握认为“数学成绩达标与否”与“每天学习数学时间能否达到一小时”有关.
的把握认为“数学成绩达标与否”与“每天学习数学时间能否达到一小时”有关.
参考公式与临界值表:K2=![]() .
.
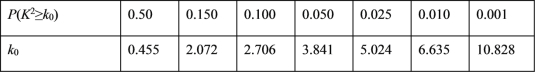
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,将
,将![]() 的图象向右平移
的图象向右平移![]() 个单位长度得到函数
个单位长度得到函数![]() 的图象,有下列叫个结论:
的图象,有下列叫个结论:
![]() 在
在![]() 单调递增;
单调递增; ![]() 为奇函数;
为奇函数;
![]() 的图象关于直线
的图象关于直线![]() 对称;
对称; ![]() 在
在![]() 的值域为
的值域为![]() .
.
其中正确的结论是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数 ,关于
,关于![]() 的方程
的方程![]() ,给出下列结论
,给出下列结论
①存在这样的实数![]() ,使得方程有3个不同的实根
,使得方程有3个不同的实根
②不存在这样的实数![]() ,是的方程有4个不同的实根
,是的方程有4个不同的实根
③存在这样的实数![]() ,是的方程有5个不同的实根
,是的方程有5个不同的实根
④不存在这样的实数![]() ,是的方程有6个不同的实根
,是的方程有6个不同的实根
其中正确的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】嫦娥四号月球探测器于2018年12月8日搭载长征三号乙运载火箭在西昌卫星发射中心发射.12日下午4点43分左右,嫦娥四号顺利进入了以月球球心为一个焦点的椭圆形轨道,如图中轨道③所示,其近月点与月球表面距离为![]() 公里,远月点与月球表面距离为
公里,远月点与月球表面距离为![]() 公里.已知月球的直径为
公里.已知月球的直径为![]() 公里,则该椭圆形轨道的离心率约为
公里,则该椭圆形轨道的离心率约为

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知直线![]() 与圆O:
与圆O:![]() 相切.
相切.
(1)直线l过点(2,1)且截圆O所得的弦长为![]() ,求直线l的方程;
,求直线l的方程;
(2)已知直线y=3与圆O交于A,B两点,P是圆上异于A,B的任意一点,且直线AP,BP与y轴相交于M,N点.判断点M、N的纵坐标之积是否为定值?若是,求出该定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司在某市的货物转运中心,拟引进智能机器人分拣系统,以提高分拣效率和降低物流成本,已知购买x台机器人的总成本为![]() 万元.
万元.

(1)若使每台机器人的平均成本最低,问应买多少台?
(2)现按(1)中的数量购买机器人,需要安排m人将邮件放在机器人上,机器人将邮件送达指定落袋格口完成分拣(如图).经实验知,每台机器人的日平均分拣量为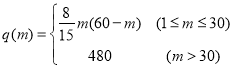 ,(单位:件).已知传统的人工分拣每人每日的平均分拣量为1200件,问引进机器人后,日平均分拣量达最大时,用人数量比引进机器人前的用人数量最多可减少百分之几?
,(单位:件).已知传统的人工分拣每人每日的平均分拣量为1200件,问引进机器人后,日平均分拣量达最大时,用人数量比引进机器人前的用人数量最多可减少百分之几?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com