
| 类型 | A规格 | B规格 | C规格 |
| 第一种钢板 | 1 | 2 | 1 |
| 第二种钢板 | 1 | 1 | 3 |
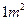 ,第二种为
,第二种为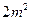 。今需要A、B、C三种规格的成品各12、15、27块.问各截这两种钢板多少张,可得所需三种规格成品,且使所用钢板面积最小?
。今需要A、B、C三种规格的成品各12、15、27块.问各截这两种钢板多少张,可得所需三种规格成品,且使所用钢板面积最小?科目:高中数学 来源:不详 题型:解答题
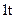 成本1 000元,运费500元,可得产品90kg,若采用乙种原料
成本1 000元,运费500元,可得产品90kg,若采用乙种原料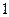 t成本1 500元,运费400元,可得产品100kg.若每日预算总成本不得超过6 000元,运费不得超过2 000元,此工厂每日最多可生产多少千克产品?
t成本1 500元,运费400元,可得产品100kg.若每日预算总成本不得超过6 000元,运费不得超过2 000元,此工厂每日最多可生产多少千克产品?查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.k≥-
| B.k≤-
| C.k>-
| D.k<-
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com