Question

6．若函数f（x）=|x²-k|的图象与函数g（x）=x-3的图象至多一个公共点，则实数k的取值范围是（　　）

• A． （-∞，3]
• B． [9，+∞）
• C． （-∞，9]
• D． （-∞，9）

Answer 1

分析 通过①当k≤0时，联立方程组，根据判别式△＜0，可得两个函数的图象无交点，故满足条件．②当k＞0时，在同一个坐标系中，画出这两个函数的图象，数形结合可得 0＜$\sqrt{k}$≤3，由此求得k的范围．综合①②可得k的范围．

解答 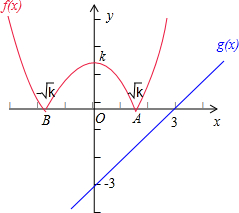解：①当k≤0时，函数f（x）=|x²-k|=x²-k，由$\left\{\begin{array}{l}{y={x}^{2}-k}\\{y=x-3}\end{array}\right.$，可得x²-x+3-k=0．
由于判别式△=1-4（3-k）=-11+4k＜0，故x²-3x+3-k=0无解，
故函数f（x）=|x²-k|的图象与函数g（x）=x-3的图象无交点，故满足条件．
②当k＞0时，在同一个坐标系中，画出函数f（x）=|x²-k|的图象（红线部分）
与函数g（x）=x-3的图象（绿线部分），
如图所示：
此时，若函数f（x）=|x²-k|的图象与函数g（x）=x-3的图象至多有一个公共点，
则有 0＜$\sqrt{k}$≤3，∴0＜k≤9．
综合①②可得，k≤9，
故选：C．

点评 本题主要考查两个函数的图象的交点个数的判断，体现了分类讨论以及数形结合的数学思想，属于中档题．