
 ��ij��ҵ������ij�ֲ�Ʒ�������ȡ100����������Щ��Ʒ��ij������ָ�꣬�ɲ�������õ�����Ƶ���ֲ�����
��ij��ҵ������ij�ֲ�Ʒ�������ȡ100����������Щ��Ʒ��ij������ָ�꣬�ɲ�������õ�����Ƶ���ֲ�����| ����ָ��ֵ���� | [75��85�� | [85��95�� | [95��105�� | [105��115�� | [115��125�� |
| Ƶ�� | 6 | 26 | 38 | 22 | 8 |
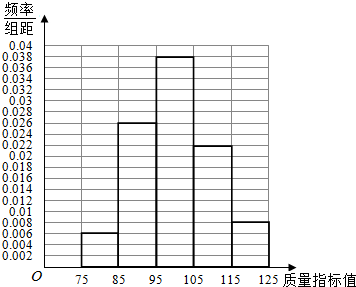
���� ��1������֪����Ƶ�ʷֲ������ɴ�������������Щ���ݵ�Ƶ�ʷֲ�ֱ��ͼ��
��2����Ƶ�ʷֲ�ֱ��ͼ���������ָ��ֵ������ƽ��������λ��λ��
��3������ָ��ֵ������95�IJ�Ʒ��ռ�����Ĺ���ֵ�����ڸù���ֵС��0.8���ʲ�����Ϊ����ҵ���������ֲ�Ʒ������ָ��ֵ������95 �IJ�Ʒ����Ҫռȫ����Ʒ80%�Ĺ涨��
��� �⣺��1������֪����Ƶ�ʷֲ���Ϊ��
| ����ָ��ֵ���� | [75��85�� | [85��95�� | [95��105�� | [105��115�� | [115��125�� |
| Ƶ�� | 6 | 26 | 38 | 22 | 8 |
| Ƶ�� | 0.06 | 0.26 | 0.38 | 0.22 | 0.08 |
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ������������ƽ��������������λ����������������Ʒ����ָ����ռ���صĹ���ֵ�ļ�����Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�3] | B�� | [9��+�ޣ� | C�� | ��-�ޣ�9] | D�� | ��-�ޣ�9�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��y=3����y'=0 | B�� | ��$y=\frac{1}{{\sqrt{x}}}$����$y'=-\frac{{\sqrt{x}}}{2}$ | C�� | ��$y=\sqrt{x}$����$y'=\frac{1}{{2\sqrt{x}}}$ | D�� | ��y=x����y'=1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{16}{23}$ | B�� | $-\frac{23}{16}$ | C�� | $\frac{16}{23}$ | D�� | $\frac{23}{16}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com