
分析 (1)化简可得解析式f(x)=sin(2x+$\frac{π}{6}$)+1,从而可求函数f(x)的单调增区间;函数f(x)的最大值,并写出f(x)取最大值时x的取值集合;
(2)由题意,f(A)=sin(2A+$\frac{π}{6}$)+1=$\frac{3}{2}$,化简可求得A的值,在△ABC中,根据余弦定理,由b+c=2,知bc≤1,即a2≥1.又由b+c>a得a<2,即可求实数a的取值范围.
解答 解:(1)f(x)=2cos2x+sin(2x-$\frac{π}{6}$)=$\frac{1}{2}$cos2x+$\frac{\sqrt{3}}{2}$sin2x+1=sin(2x+$\frac{π}{6}$)+1,
2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,可得函数f(x)的单调增区间[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$](k∈Z),
函数f(x)的最大值为2.
当且仅当sin(2x+$\frac{π}{6}$)=1,即2x+$\frac{π}{6}$=2kπ+$\frac{π}{2}$,即x=kπ+$\frac{π}{6}$(k∈Z)时取到.
所以函数最大值为2时x的取值集合为{x|x=kπ+$\frac{π}{6}$,k∈Z}.…(6分)
(2)由题意,f(A)=sin(2A+$\frac{π}{6}$)+1=$\frac{3}{2}$,化简得sin(2A+$\frac{π}{6}$)=$\frac{1}{2}$.
∵A∈(0,π),∴2A+$\frac{π}{6}$=$\frac{5π}{6}$,
∴A=$\frac{π}{3}$.
在△ABC中,根据余弦定理,得a2=b2+c2-bc=(b+c)2-3bc.
由b+c=2,知bc≤1,即a2≥1.
∴当b=c=1时,取等号.
又由b+c>a得a<2.
所以a的取值范围是[1,2 ).…(12分)
点评 本题主要考查三角函数中的恒等变换应用,余弦定理的应用,不等式的解法,属于中档题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:填空题
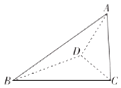 已知三棱锥A-BCD的四个顶点A、B、C、D都在球O的表面上,AC⊥平面BCD,BC⊥CD,且AC=$\sqrt{3}$,BC=2,CD=$\sqrt{5}$,则球O的表面积为12π.
已知三棱锥A-BCD的四个顶点A、B、C、D都在球O的表面上,AC⊥平面BCD,BC⊥CD,且AC=$\sqrt{3}$,BC=2,CD=$\sqrt{5}$,则球O的表面积为12π.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 212-57 | B. | 211-47 | C. | 210-38 | D. | 29-30 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
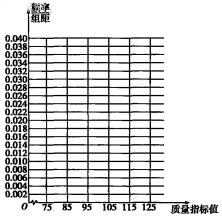 从某企业生产的某种产品中随机抽取100件,测量这些产品的某项质量指标,由测量结果得到如下频数分布表:
从某企业生产的某种产品中随机抽取100件,测量这些产品的某项质量指标,由测量结果得到如下频数分布表:| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 26 | 38 | 22 | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
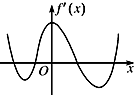
| A. | 无极大值点,有四个极小值点 | B. | 有三个极大值点,两个极小值点 | ||
| C. | 有两个极大值点,两个极小值点 | D. | 有四个极大值点,无极小值点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
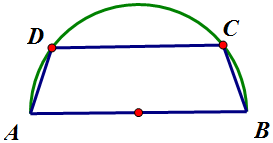 有一块半径为2的半圆形钢板,计划裁剪成等腰梯形ABCD的形状,它的下底AB是半圆的直径,上底CD的端点在半圆上.
有一块半径为2的半圆形钢板,计划裁剪成等腰梯形ABCD的形状,它的下底AB是半圆的直径,上底CD的端点在半圆上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p:?x∈[0,2π],sinx≥1 | B. | ¬p:?x∈[-2π,0],sinx>1 | ||
| C. | ¬p:?x∈[0,2π],sinx>1 | D. | ¬p:?x∈[-2π,0],sinx>1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com