
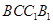 是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线
是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线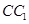 的中点,已知
的中点,已知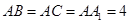
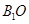 ⊥平面
⊥平面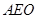 ;
;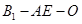 的余弦值.
的余弦值.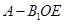 的体积.
的体积. 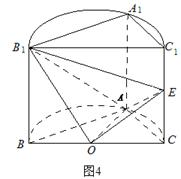
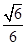 (Ⅲ)8
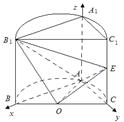
(Ⅲ)8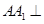 平面ABC,∠
平面ABC,∠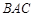 =90°,
=90°,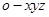 ,
,
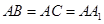 =4,
=4,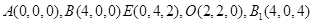
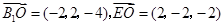 ,
,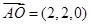
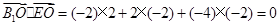 ,∴
,∴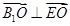 ,∴
,∴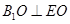
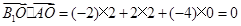 , ∴
, ∴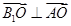 ,∴
,∴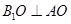

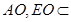 平面
平面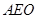 ∴
∴ 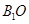 ⊥平面
⊥平面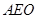 (5分)
(5分)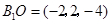 ,设平面 B1AE的法向量为
,设平面 B1AE的法向量为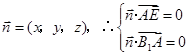 , 即
, 即
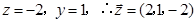
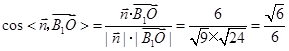
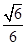 (10分)
(10分)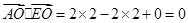 ,∴
,∴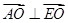 , ∴
, ∴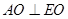
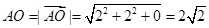 ,
,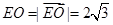
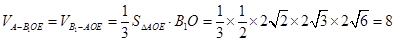 (14 分)
(14 分)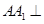 平面ABC,∠
平面ABC,∠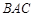 =90°,
=90°,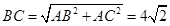 ,∴
,∴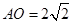
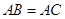 ,O为底面圆心,∴BC⊥AO,又∵B1B⊥平面ABC,可证B1O⊥AO,
,O为底面圆心,∴BC⊥AO,又∵B1B⊥平面ABC,可证B1O⊥AO, 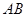 =
=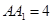 ,则
,则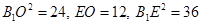 ,∴
,∴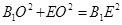
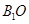 ⊥平面
⊥平面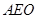 ; (5分)
; (5分)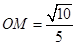 ,
, 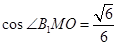
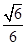 (10分)
(10分)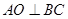
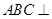 平面
平面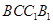 ,且平面
,且平面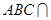 平面
平面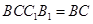 ,
,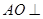 平面
平面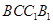 , 故
, 故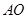 是三棱锥
是三棱锥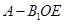 的高
的高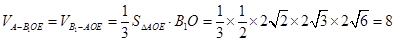 (14分)
(14分)

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:高中数学 来源:不详 题型:单选题

| A.3 | B. | C. | D.6 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
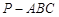 ,
,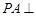 平面
平面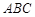 ,
,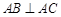 ,
,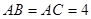 ,
,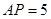 .
.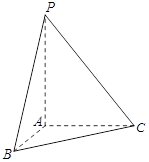
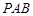 (及其内部)绕
(及其内部)绕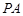 所在直线旋转一周形成一几何体,求该几何体的体积
所在直线旋转一周形成一几何体,求该几何体的体积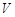 ;
; 的余弦值.
的余弦值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com