
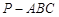 ,
,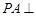 平面
平面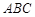 ,
,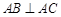 ,
,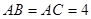 ,
,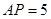 .
.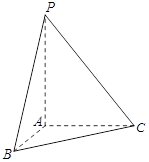
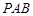 (及其内部)绕
(及其内部)绕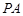 所在直线旋转一周形成一几何体,求该几何体的体积
所在直线旋转一周形成一几何体,求该几何体的体积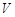 ;
; 的余弦值.
的余弦值. . (Ⅱ)
. (Ⅱ) .
.  ,高为
,高为 .
.  . ………………5分
. ………………5分 ,
, ,
, ,
, .于是
.于是 ,
, .………………7分
.………………7分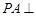 平面
平面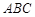 ,得平面
,得平面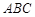 的一个法向量
的一个法向量 .……8分
.……8分 是平面
是平面 的一个法向量.
的一个法向量. ,
, ,所以
,所以 ,
, ,
, ,
, ,解得
,解得 ,
, ,取
,取 ,得
,得 .…10分
.…10分 与
与 的夹角为
的夹角为 ,则
,则 . ………12分
. ………12分 是个锐角,它的余弦值为
是个锐角,它的余弦值为 . ………………13分
. ………………13分

科目:高中数学 来源:不详 题型:解答题
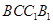 是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线
是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线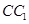 的中点,已知
的中点,已知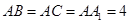
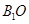 ⊥平面
⊥平面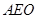 ;
;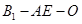 的余弦值.
的余弦值.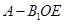 的体积.
的体积. 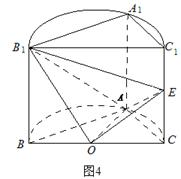
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
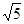 ,BC=AD=
,BC=AD=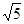 。现沿着其对角线AC将D点向上翻折,使得二面角D—AC—B为直二面角。
。现沿着其对角线AC将D点向上翻折,使得二面角D—AC—B为直二面角。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com