
ΓΨΧβΡΩΓΩΡ≥―ß–Θ‘Ύ“Μ¥ΈΒΎΕΰΩΈΧΟΜνΕ·÷–Θ§ΧΊ“β…η÷ΟΝΥΙΐΙΊ÷«ΝΠ”ΈœΖΘ§”ΈœΖΙ≤ΈεΙΊΘ°ΙφΕ®ΒΎ“ΜΙΊΟΜΙΐ’ΏΟΜΫ±άχΘ§Ιΐ![]()
![]() ΙΊ’ΏΫ±άχ
ΙΊ’ΏΫ±άχ![]() Φΰ–ΓΫ±ΤΖΘ®Ϋ±ΤΖΕΦ“Μ―υΘ©Θ°œ¬ΆΦ «–ΓΟς‘Ύ10¥ΈΙΐΙΊ”ΈœΖ÷–ΙΐΙΊ ΐΒΡΧθ–ΈΆΦΘ§“‘¥ΥΤΒ¬ ΙάΦΤΗ≈¬ Θ°
Φΰ–ΓΫ±ΤΖΘ®Ϋ±ΤΖΕΦ“Μ―υΘ©Θ°œ¬ΆΦ «–ΓΟς‘Ύ10¥ΈΙΐΙΊ”ΈœΖ÷–ΙΐΙΊ ΐΒΡΧθ–ΈΆΦΘ§“‘¥ΥΤΒ¬ ΙάΦΤΗ≈¬ Θ°

(Δώ)ΙάΦΤ–ΓΟς‘Ύ1¥Έ”ΈœΖ÷–ΥυΒΟΫ±ΤΖ ΐΒΡΤΎΆϊ÷ΒΘΜ
(Δρ)ΙάΦΤ–ΓΟς‘Ύ3 ¥Έ”ΈœΖ÷–÷Ν…ΌΙΐΝΫΙΊΒΡΤΫΨυ¥Έ ΐΘΜ
(Δσ)ΙάΦΤ–ΓΟς‘Ύ3 ¥Έ”ΈœΖ÷–ΥυΒΟΫ±ΤΖ≥§Ιΐ30ΦΰΒΡΗ≈¬ Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©4ΘΜΘ®2Θ©2.1ΘΜΘ®3Θ©0.031
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©Ν–≥ω–ΓΟς‘Ύ1¥Έ”ΈœΖ÷–ΥυΒΟΫ±ΤΖ ΐΈΣ![]() ΒΡΖ÷≤ΦΝ–Θ§ΗυΨίΖ÷≤ΦΝ–«σ≥ωΤΎΆϊΦ¥Ω…ΘΜΘ®2Θ©”…±μΩ…ΒΟ–ΓΟς‘Ύ1 ¥Έ”ΈœΖ÷–÷Ν…ΌΙΐΝΫΙΊΒΡΗ≈¬ ΈΣ0.7Θ§”…ΕΰœνΖ÷≤ΦΩ…ΒΟΫαΙϊΘΜΘ®3Θ©Ζ÷ΈωΩ…ΒΟ–ΓΟς‘Ύ3 ¥Έ”ΈœΖ÷–ΥυΒΟΫ±ΤΖ≥§Ιΐ30ΦΰΚ§»ΐάύΘΚ«ΓΚΟ“Μ¥Έ
ΒΡΖ÷≤ΦΝ–Θ§ΗυΨίΖ÷≤ΦΝ–«σ≥ωΤΎΆϊΦ¥Ω…ΘΜΘ®2Θ©”…±μΩ…ΒΟ–ΓΟς‘Ύ1 ¥Έ”ΈœΖ÷–÷Ν…ΌΙΐΝΫΙΊΒΡΗ≈¬ ΈΣ0.7Θ§”…ΕΰœνΖ÷≤ΦΩ…ΒΟΫαΙϊΘΜΘ®3Θ©Ζ÷ΈωΩ…ΒΟ–ΓΟς‘Ύ3 ¥Έ”ΈœΖ÷–ΥυΒΟΫ±ΤΖ≥§Ιΐ30ΦΰΚ§»ΐάύΘΚ«ΓΚΟ“Μ¥Έ![]() ΚΆΝΫ¥Έ
ΚΆΝΫ¥Έ![]() Θ§«ΓΚΟΕΰ¥Έ
Θ§«ΓΚΟΕΰ¥Έ![]() Θ§«ΓΚΟ»ΐ¥Έ
Θ§«ΓΚΟ»ΐ¥Έ![]() Θ§”…ΜΞ≥β ¬ΦΰΦΑœύΜΞΕάΝΔ ¬ΦΰΖΔ…ζΒΡΗ≈¬ Ω…ΒΟΫαΙϊ.
Θ§”…ΜΞ≥β ¬ΦΰΦΑœύΜΞΕάΝΔ ¬ΦΰΖΔ…ζΒΡΗ≈¬ Ω…ΒΟΫαΙϊ.
‘ΧβΫβΈωΘΚ (1)…η–ΓΟς‘Ύ1¥Έ”ΈœΖ÷–ΥυΒΟΫ±ΤΖ ΐΈΣ![]() Θ§‘ρ
Θ§‘ρ![]() ΒΡΖ÷≤ΦΝ–ΈΣ
ΒΡΖ÷≤ΦΝ–ΈΣ
| 0 | 1 | 2 | 4 | 8 | 16 |
P | 0.1 | 0.2 | 0.3 | 0.2 | 0.1 | 0.1 |
![]() ΒΡΤΎΆϊ÷Β
ΒΡΤΎΆϊ÷Β![]() ΘΜ
ΘΜ
(2)–ΓΟς‘Ύ1 ¥Έ”ΈœΖ÷–÷Ν…ΌΙΐΝΫΙΊΒΡΗ≈¬ ΈΣ0.7Θ§
…η–ΓΟς‘Ύ3 ¥Έ”ΈœΖ÷–÷Ν…ΌΙΐΝΫΙΊΒΡ¥Έ ΐΈΣXΘ§Ω…÷Σ![]() Θ§
Θ§
‘ρXΒΡΤΫΨυ¥Έ ΐ![]() ΘΜ
ΘΜ
(3)–ΓΟς‘Ύ3 ¥Έ”ΈœΖ÷–ΥυΒΟΫ±ΤΖ≥§Ιΐ30ΦΰΚ§»ΐάύΘΚ«ΓΚΟ“Μ¥Έ![]() ΚΆΝΫ¥Έ
ΚΆΝΫ¥Έ![]() Θ§«ΓΚΟΕΰ¥Έ
Θ§«ΓΚΟΕΰ¥Έ![]() Θ§«ΓΚΟ»ΐ¥Έ
Θ§«ΓΚΟ»ΐ¥Έ![]() Θ§
Θ§
![]() Θ§
Θ§
![]() =
=![]() Θ§
Θ§
![]()
Υυ“‘–ΓΟς‘Ύ3 ¥Έ”ΈœΖ÷–ΥυΒΟΫ±ΤΖ≥§Ιΐ30ΦΰΒΡΗ≈¬ ΈΣ![]() Θ°
Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΙϊΕ®“ε‘ΎΘ®©¹ΓόΘ§0Θ©Γ»Θ®0Θ§+ΓόΘ©…œΒΡΤφΚ· ΐfΘ®xΘ©Θ§‘ΎΘ®0Θ§+ΓόΘ©ΡΎ «ΦθΚ· ΐΘ§”÷”–fΘ®3Θ©=0Θ§‘ρxfΘ®xΘ©ΘΦ0ΒΡΫβΦ·ΈΣΘ® Θ©
A.{x|©¹3ΘΦxΘΦ0ΜρxΘΨ3}
B.{x|xΘΦ©¹3Μρ0ΘΦxΘΦ3}
C.{x|©¹3ΘΦxΘΦ0Μρ0ΘΦxΘΦ3}
D.{x|xΘΦ©¹3ΜρxΘΨ3}
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬Ν–Κ· ΐ÷–Θ§ «≈ΦΚ· ΐΘ§«“‘Ύ«χΦδΘ®0Θ§1Θ©…œΈΣ‘ωΚ· ΐΒΡ «Θ® Θ©
A.y=|x|
B.y=1©¹x
C.y= ![]()
D.y=©¹x2+4
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥―ß–Θ‘Ύ“Μ¥ΈΒΎΕΰΩΈΧΟΜνΕ·÷–Θ§ΧΊ“β…η÷ΟΝΥΙΐΙΊ÷«ΝΠ”ΈœΖΘ§”ΈœΖΙ≤ΈεΙΊΘ°ΙφΕ®ΒΎ“ΜΙΊΟΜΙΐ’ΏΟΜΫ±άχΘ§Ιΐ![]() ΙΊ’ΏΫ±άχ
ΙΊ’ΏΫ±άχ![]() Φΰ–ΓΫ±ΤΖΘ®Ϋ±ΤΖΕΦ“Μ―υΘ©Θ°œ¬ΆΦ «–ΓΟς‘Ύ10¥ΈΙΐΙΊ”ΈœΖ÷–ΙΐΙΊ ΐΒΡΧθ–ΈΆΦΘ§“‘¥ΥΤΒ¬ ΙάΦΤΗ≈¬ Θ°
Φΰ–ΓΫ±ΤΖΘ®Ϋ±ΤΖΕΦ“Μ―υΘ©Θ°œ¬ΆΦ «–ΓΟς‘Ύ10¥ΈΙΐΙΊ”ΈœΖ÷–ΙΐΙΊ ΐΒΡΧθ–ΈΆΦΘ§“‘¥ΥΤΒ¬ ΙάΦΤΗ≈¬ Θ°
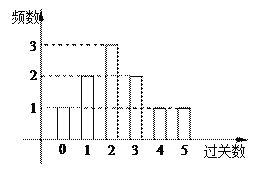
(Δώ)«σ–ΓΟς‘Ύ’β °¥Έ”ΈœΖ÷–ΥυΒΟΫ±ΤΖ ΐΒΡΨυ÷ΒΘΜ
(Δρ)ΙφΕ®Ιΐ»ΐΙΊ’Ώ≤≈ΡήΆφΝμ“ΜΗωΗΏΦΕ±πΒΡ”ΈœΖΘ§ΙάΦΤ–ΓΟς“Μ¥Έ”ΈœΖΚσΡήΆφΝμ“ΜΗω”ΈœΖΒΡΗ≈¬ ΘΜ
(Δσ)“―÷Σ–ΓΟς‘ΎΡ≥ΥΡ¥Έ”ΈœΖ÷–ΥυΙΐΙΊ ΐΈΣ{2,2,3,4}Θ§–Γ¥œ‘ΎΡ≥ΥΡ¥Έ”ΈœΖ÷–ΥυΙΐΙΊ ΐΈΣ{3,3,4,5}Θ§œ÷¥”÷–Ης―Γ“Μ¥Έ”ΈœΖΘ§«σ–ΓΟςΚΆ–Γ¥œΥυΒΟΫ±ΤΖΉή ΐ≥§Ιΐ10ΒΡΗ≈¬ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ―Γ–ό4![]() 4ΘΚΉχ±ξœΒ”κ≤Έ ΐΖΫ≥Χ
4ΘΚΉχ±ξœΒ”κ≤Έ ΐΖΫ≥Χ
‘Ύ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§“―÷Σ÷±œΏl1ΘΚ
÷–Θ§“―÷Σ÷±œΏl1ΘΚ ![]() Θ®
Θ®![]() Θ§
Θ§ ![]() Θ©Θ§≈ΉΈοœΏCΘΚ
Θ©Θ§≈ΉΈοœΏCΘΚ  Θ®tΈΣ≤Έ ΐΘ©Θ°“‘‘≠Βψ
Θ®tΈΣ≤Έ ΐΘ©Θ°“‘‘≠Βψ![]() ΈΣΦΪΒψΘ§
ΈΣΦΪΒψΘ§ ![]() ÷αΒΡΖ«ΗΚΑκ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒΘ°
÷αΒΡΖ«ΗΚΑκ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒΘ°
Θ®ΔώΘ©«σ÷±œΏl1 ΚΆ≈ΉΈοœΏCΒΡΦΪΉχ±ξΖΫ≥ΧΘΜ
Θ®ΔρΘ©»τ÷±œΏl1 ΚΆ≈ΉΈοœΏCœύΫΜ”ΎΒψAΘ®“λ”Ύ‘≠ΒψOΘ©Θ§Ιΐ‘≠ΒψΉς”κl1¥Ι÷±ΒΡ÷±œΏl2Θ§l2ΚΆ≈ΉΈοœΏCœύΫΜ”ΎΒψBΘ®“λ”Ύ‘≠ΒψOΘ©Θ§«σΓςOABΒΡΟφΜΐΒΡΉν–Γ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() .
.
Θ®1Θ©Β±![]() ±Θ§«σ
±Θ§«σ![]() ΒΡΒΞΒς«χΦδΘΜ
ΒΡΒΞΒς«χΦδΘΜ
Θ®2Θ©»τ![]() ±Θ§≤ΜΒ» Ϋ
±Θ§≤ΜΒ» Ϋ![]() ≥…ΝΔΘ§«σ Β ΐ
≥…ΝΔΘ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈß.
ΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ÷±Ϋ«Χί–Έ![]() ÷–Θ§
÷–Θ§ ![]() //
// ![]() Θ§
Θ§ ![]() ΓΆ
ΓΆ![]() Θ§
Θ§ ![]() ΓΆ
ΓΆ![]() , Βψ
, Βψ![]() «
«![]() ±ΏΒΡ÷–Βψ, ΫΪΓς
±ΏΒΡ÷–Βψ, ΫΪΓς![]() ―Ί
―Ί![]() ’έΤπΘ§ ΙΤΫΟφ
’έΤπΘ§ ΙΤΫΟφ![]() ΓΆΤΫΟφ
ΓΆΤΫΟφ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() ,
, ![]() ,
, ![]() , ΒΟΒΫ»γΆΦΥυ ΨΒΡΦΗΚΈΧε.
, ΒΟΒΫ»γΆΦΥυ ΨΒΡΦΗΚΈΧε.
Θ®ΔώΘ©«σ÷ΛΘΚ ![]() ΓΆΤΫΟφ
ΓΆΤΫΟφ![]() ΘΜ
ΘΜ
Θ®ΔρΘ©»τ![]() Θ§
Θ§ ![]() Θ§«σΕΰΟφΫ«
Θ§«σΕΰΟφΫ«![]() ΒΡ¥σ–Γ.
ΒΡ¥σ–Γ.


≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“ΜΗωΦΗΚΈΧεΒΡ»ΐ ”ΆΦ»γΆΦΥυ ΨΘ§Τδ÷–’ΐ ”ΆΦ «“ΜΗω’ΐ»ΐΫ«–ΈΘ§‘ρ’βΗωΦΗΚΈΧεΒΡΧεΜΐ « Θ§±μΟφΜΐ « Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐy=x2©¹ax©¹3Θ®©¹5ΓήxΓή5Θ©
Θ®1Θ©»τa=2Θ§«σΚ· ΐΒΡΉν÷ΒΘΜ
Θ®2Θ©»τΚ· ΐ‘ΎΕ®“ε”ρΡΎ «ΒΞΒςΚ· ΐΘ§«σa»Γ÷ΒΒΡΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com