
 ,圆心角为60°的扇形的弧上任取一点P,作扇形的内接矩形PNMQ,使点Q在OA上,点N,M在OB上.设矩形PNMQ的面积为y,∠POB=θ,将y表示成θ的函数关系式,并求出y的最大值.
,圆心角为60°的扇形的弧上任取一点P,作扇形的内接矩形PNMQ,使点Q在OA上,点N,M在OB上.设矩形PNMQ的面积为y,∠POB=θ,将y表示成θ的函数关系式,并求出y的最大值.
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
 如图所示,在半径为
如图所示,在半径为| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:044
如图所示,在半径为
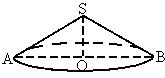
50m的圆形广场中央O的上空安装了一个照明光源S,S射向地面的光束呈圆锥形,其轴截面SAB的顶角120°.求光源高出地面的高度
SO.
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学必修三3.3几何概型练习卷(二)(解析版) 题型:填空题
如图所示,在半径为1的半圆内放置一个边长为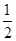 的正方形ABCD,向半圆内任投一点,则点落在正方形内的概率为________.
的正方形ABCD,向半圆内任投一点,则点落在正方形内的概率为________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com