练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

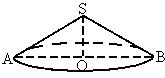
    如图所示，在半径为50m的圆形广场中央O的上空安装了一个照明光源S，S射向地面的光束呈圆锥形，其轴截面SAB的顶角120°．

    求光源高出地面的高度SO．
    答案：28.9m
    解析：

    解：在△SAB中，SA=SB，，

    ∵SO⊥AB，O为AB的中点，且，在Rt△ASO中，OA=50m，

    ，设SO=x，则AS=2x，由勾股定理得，即，解得

    ．

    答：光源S离地面的垂直高度为28.9m．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （坐标系与参数方程选做题）在极坐标系中，定点A（2，π），动点B在直线ρsin(θ+
    π
    4
    )=
    		2
    2
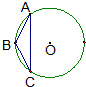    上运动，则线段AB的最精英家教网短长度为
     

    （不等式选讲选做题）设函数f（x）=|x-1|+|x-2|，则f（x）的最小值为
     

    （几何证明选讲选做题） 如图所示，等腰三角形ABC的底边AC长为6，其外接圆的半径长为5，则三角形ABC的面积是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

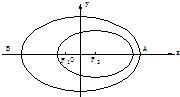    精英家教网2003年10月15日9时，“神舟”五号载人飞船发射升空，于9时9分50秒准确进入预定轨道，开始巡天飞行．该轨道是以地球的中心F2为一个焦点的椭圆．选取坐标系如图所示，椭圆中心在原点．近地点A距地面200km，远地点B距地面350km．已知地球半径R=6371km．
    （I）求飞船飞行的椭圆轨道的方程；
    （II）飞船绕地球飞行了十四圈后，于16日5时59分返
    回舱与推进舱分离，结束巡天飞行，飞船共巡天飞行了约6×105km，问飞船巡天飞行的平均速度是多少km/s？
    （结果精确到1km/s）（注：km/s即千米/秒）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图所示，直角坐标系xOy建立在湖泊的某一恰当位置，现准备在湖泊的一侧修建一条观光大道，它的前一段MD是以O为圆心，OD为半径的圆弧，后一段DBC是函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
    π
    2
     ），x∈[4，8]时的图象，图象的最高点为B(5，
    8
    3
    )
    （Ⅰ）求函数y=sin（ωx+φ）的解析式；
    （Ⅱ）若在湖泊内修建如图所示的矩形水上乐园OEPF，其中折线FPE为水上赛艇线路，问点P落在圆弧MD上何处时赛艇线路最长？精英家教网

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图为一个观览车示意图，该观览车半径为4.8m，圆上最低点与地面距离为0.8m，60秒转动一圈，图中OA与地面垂直，以OA为始边，逆时针转动θ角到OB，设B点与地面距离为h．
    （1）在如图所示直角坐标系中，求h与θ间关系的函数解析式；
    （2）设从OA开始转动，经过t秒到达OB，求h与t间关系的函数解析式；
    （3）填写下列表格：
    θ 0° 30° 60° 90° 120° 150° 180°
    h（m）
    t（s） 0 5 10 15 20 25 30
    h（m）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （三选一，考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
    （1）（坐标系与参数方程选做题）在直角坐标系中圆C的参数方程为
    x=1+2cosθ
    y=
    		3
    +2sinθ
    （θ为参数），则圆C的普通方程为
    (x-1)2+(y-
    		3
    )2=4
    (x-1)2+(y-
    		3
    )2=4
    ．
    （2）（不等式选讲选做题）设函数f（x）=|2x+1|-|x-4|，则不等式f（x）＞2的解集为
    {x|x＜-7或x＞
    5
    3
    }
    {x|x＜-7或x＞
    5
    3
    }
    ．
    （3）（几何证明选讲选做题） 如图所示，等腰三角形ABC的底边AC长为6，其外接圆的半径长为5，则三角形ABC的面积是
    3
    3
    ．

    查看答案和解析>>

    同步练习册答案