
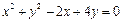 按向量a=(-1,2)平移后得到⊙O,直线l与⊙O相交于A、B两点,若在⊙O上存在点C,使
按向量a=(-1,2)平移后得到⊙O,直线l与⊙O相交于A、B两点,若在⊙O上存在点C,使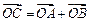 =λa,求直线l的方程及对应的点C的坐标.
=λa,求直线l的方程及对应的点C的坐标.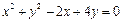 化为标准方程为
化为标准方程为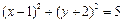 ,
,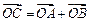 =λa,且|
=λa,且|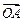 |=|
|=|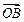 |,∴
|,∴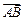 ⊥
⊥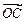 ,
,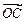 ∥a.
∥a.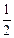 .设直线l的方程为y=
.设直线l的方程为y=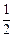 x+m,联立,得
x+m,联立,得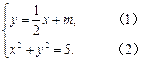
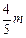 ,y1+y2=
,y1+y2=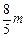 ,
,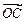 =(-
=(-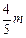 ,
,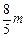 ).
).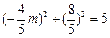 ,解之,得
,解之,得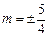 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
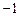 ),B(5,3),并且被直线
),B(5,3),并且被直线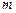 :
: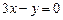 平分圆的面积.
平分圆的面积.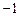 ),且斜率为
),且斜率为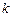 的直线
的直线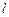 与圆C有两个不同的公共点,求实数
与圆C有两个不同的公共点,求实数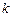 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
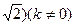 与圆O:x2+y2=4相交于A,B两点,O为坐标原点,△AOB的面积为S。(1)试将S表示为k的函数S(k),并求出它的义域;求S的最大值,并求出此时的k值。
与圆O:x2+y2=4相交于A,B两点,O为坐标原点,△AOB的面积为S。(1)试将S表示为k的函数S(k),并求出它的义域;求S的最大值,并求出此时的k值。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
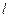 的距离为2,Q是
的距离为2,Q是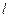 上一动点,⊙Q与⊙P相外切,⊙Q交
上一动点,⊙Q与⊙P相外切,⊙Q交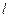 于M、N两点,对于任意直径MN,平面上恒有一定点A,使得∠MAN为定值。求∠MAN的度数。
于M、N两点,对于任意直径MN,平面上恒有一定点A,使得∠MAN为定值。求∠MAN的度数。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.在圆外 | B.在圆上 | C.在圆内 | D.不确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com